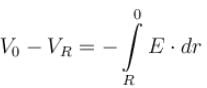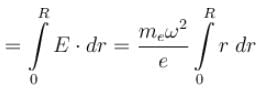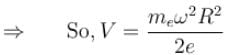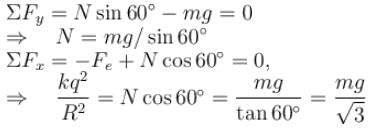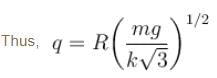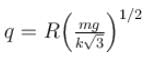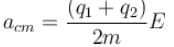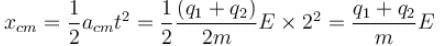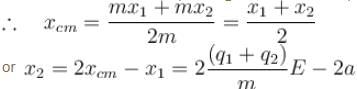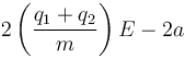Electrostatics MCQ Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Electrostatics MCQ Level - 2
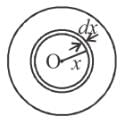
The electric field inside a sphere which carries a volume charge density proportional to the distance from the origin ρ = α r, (α is a constant) is:
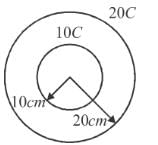
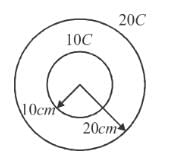
Two concentric uniformly charged spheres of radius 10 cm and 20 cm are arranged as shown in the figure. Potential difference between the spheres is :

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
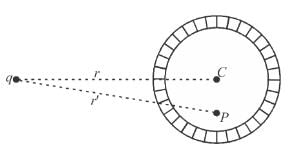
A neutral conducting spherical shell is kept near a charge q as shown. The potential at point P due to the induced charges is

An infinitely long plate has surface charge density ρ. As shown in the figure, a point charge q is moved from A to B. Net work done by electric field is:
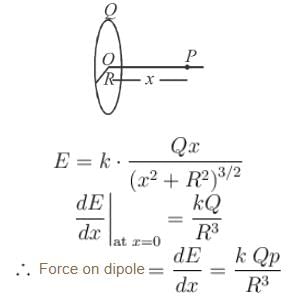
A dipole of dipole moment p is kept at the centre of a ring of radius R and charge Q. The dipole moment has direction along the axis of the ring. The resultant force on the ring due to the dipole is:
In the figure shown. A is a fixed charge. B (of mass m) is given a velocity v perpendicular to line AB. At this moment the radius of curvature of the resultant path of B is
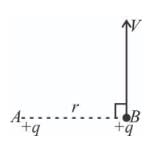
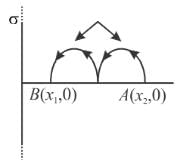
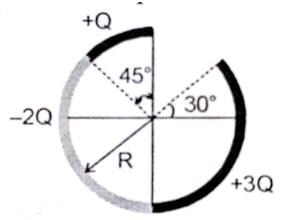
Figure shows three circular arcs, each of radius R and total charge as indicated. The net electric potential at the centre of curvature is :
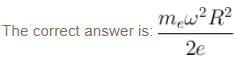
A conducting disc of radius R rotates about its axis with an angular velocity ω. Then the potential difference between the centre of the disc and its edge is (no magnetic field is present):
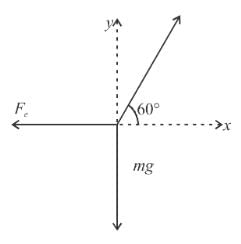
Two identical small balls each have a mass m and charge q. When placed in a hemispherical bowl of radius R with friction less, non-conducting walls, the beads move and at equilibrium, the line joining the balls is horizontal and the distance between them is R (figure). Neglect any induced charge on the hemispherical bowl. Then the charge on each bead is: (here, 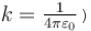
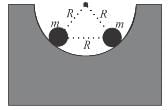
Two positively charged particles of charges q1 and q2 have mass m each. A uniform electric field having magnitude E exists in positive x direction as shown in the figure. The given two charged particles are released from rest at t = 0 as shown in the figure. If position of q1 at t = 2sec is given by coordinate (+2a, 0) then the x-coordinate of q2 at t = 2sec is (neglect gravitational interaction between the particles)


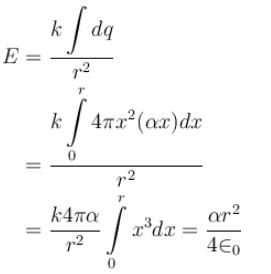

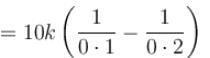
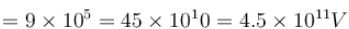
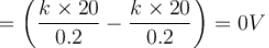
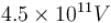
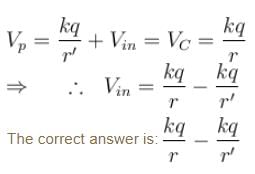
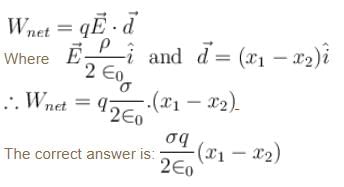
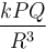
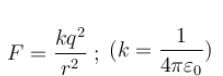
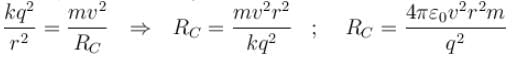
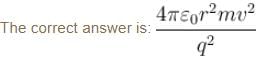
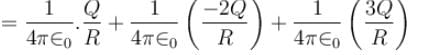
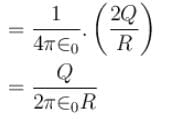
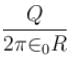
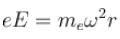 (Balancing of forces of e–)
(Balancing of forces of e–)