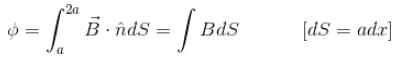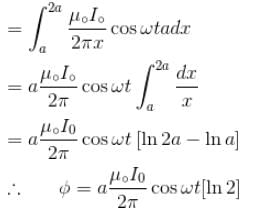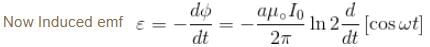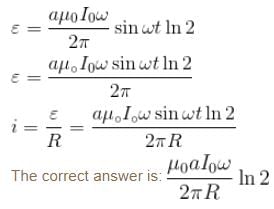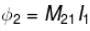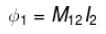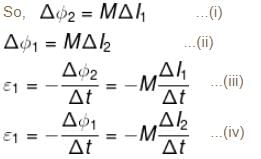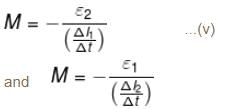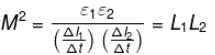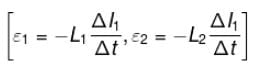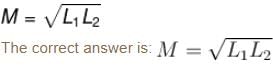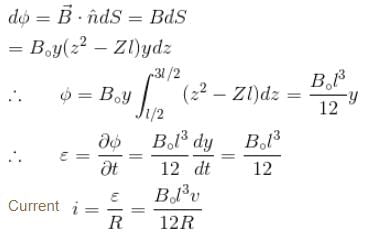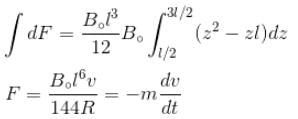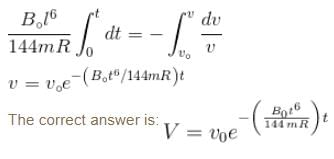Faraday's Law MCQ Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Faraday's Law MCQ Level - 2
The current in inner coil is i = 2t2, as shown in figure. The current induced in the outer coil has a resistance of R.
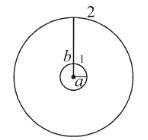

A circular loop of radius a is made of a single turn of thin conducting wire. The self inductance of this loop is L. If the number of turns in the loop is increased from 1 to 8, the self inductance would be :
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A large circular coil of N turns and radius R carries a time varying current I = I0 sin (ωt). A small circular coil of n turns and radius r (r << R) is placed at the center of the large coil such that the coils are concentric and coplanar. The induced emf in the small coil :
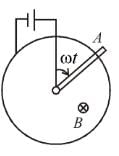
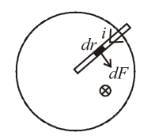
A metal disc of radius a rotates with an angular velocity ω about an axis perpendicular to its plane passing through its centre in a magnetic field of induction B acting perpendicular to the plane of the disc. The induced emf between the rim and axis of the disc.
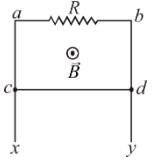
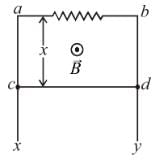
A wire coil of length l, mass m, is sliding without friction on conducting rail ax and by as shown in figure. The vertical rails are connected to one another via an external resistance R. The entire circuit is placed in a region of space having a uniform magnetic field B. The field is perpendicular to the plane of circuit and directed outwards. The steady speed of rod cd is
A loop is formed by two parallel conductor connected by a solenoid with inductance L and a conducting rod of mass m which can freely (without friction) side over the conductors. The conductors are located in horizontal plane in a uniform vertical magnetic field B. The distance between the conductor is l. Then angular frequency of rod.
A conducting rod of length a is rotating with constant angular speed ω about its perpendicular bisector. A uniform magnetic field B exist parallel to the axis of rotation. The emf induced between two ends of the rod is.
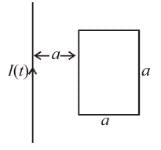
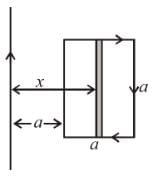
An infinite long wire carrying a current I(t) = I0 cos(ωt) is placed at a distance a from a square loop of side a in the figure. If the resistance of the loop is R, then the amplitude of the induced current in the loop is :
Two coil of self inductance L1 and L2 are placed closed to each other so that total flux in one coil is completely linked with other. If M is the mutual inductance between them, then :
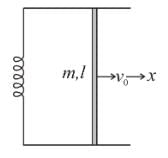
Two parallel rails separated by a distance l are connected through a resistance R in yz plane. Magnetic field 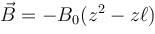 is present in the direction perpendicular to the plane of the rails. A conducting rod of mass. m placed on the rails and given a velocity of v0 parallel to the plane of rails. The expression for the velocity.
is present in the direction perpendicular to the plane of the rails. A conducting rod of mass. m placed on the rails and given a velocity of v0 parallel to the plane of rails. The expression for the velocity.


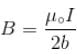
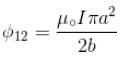
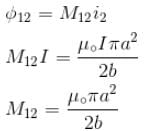
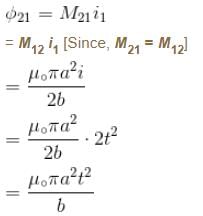
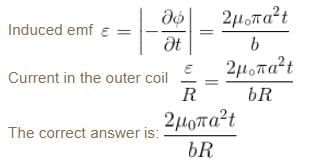
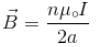
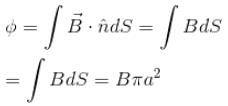
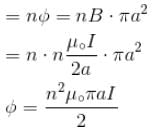
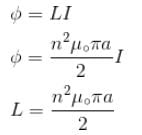
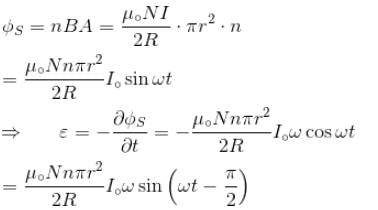
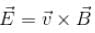
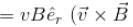 will lie in radially outward direction)
will lie in radially outward direction)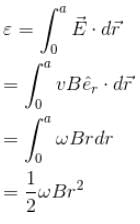
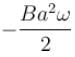
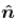 lying in same direction as
lying in same direction as 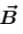
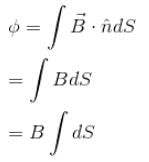
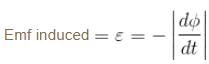
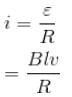
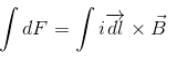
 are perpendicular
are perpendicular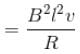 (forward up the incline)
(forward up the incline)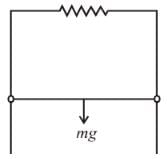
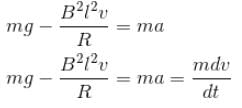
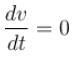
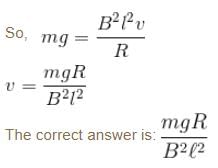
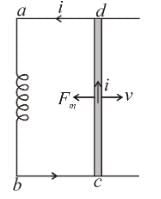
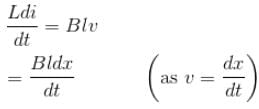
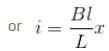
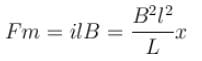
 so from Newton’s second law we an write
so from Newton’s second law we an write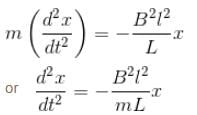
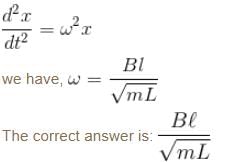
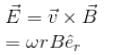
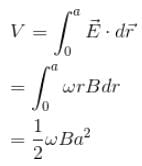
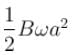
 lie in same direction,
lie in same direction, 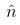 is unit normal to surface.
is unit normal to surface.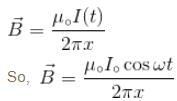
 element
element