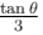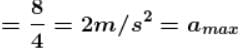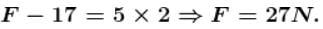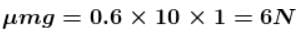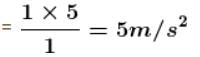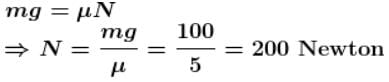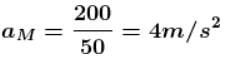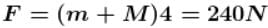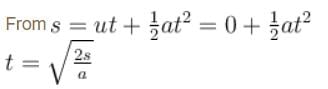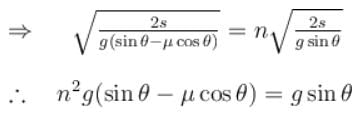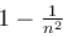Friction Force MCQ Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Friction Force MCQ Level - 2
A box of mass 8kg is placed on a rough inclined plane of inclination θ. Its downward motion can be prevented by applying an upward pull F and it can be made to slide upwards by applying a force 2F. The coefficient of friction between the box and the inclined plane is
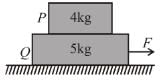
The coefficient of friction between 4kg and 5kg blocks is 0.2 and between 5kg blocks and ground is 0.1 respectively. Choose the correct statement :

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A block of mass 1kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5 m/s2, the friction force acting on the block is :
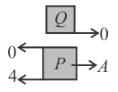
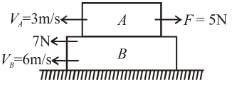
In the following figure, find the direction of friction on the blocks and ground respectively.
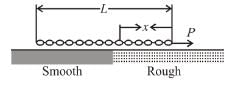
A chain of length L is placed on a horizontal surface as shown in figure. At any instant x is the length of chain on rough surface and the remaining portion lies on smooth surface. Initially x = 0. A horizontal force P is applied to the chain (as shown in the figure). In the duration x changes from x = 0 to x = L, for chain to move with constant speed :
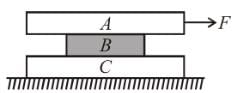
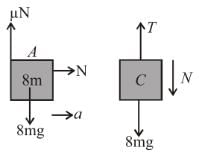
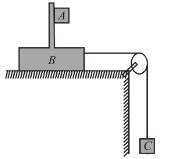
In the arrangement shown in the figure mass of the block B and A are 2m, 8m respectively. Surface between B and floor is smooth. The block B is connected to block C by means of a pulley. If the whole system is released then the minimum value of mass of the block C so that the block A remains stationary with respect to B is :
(Co-efficient of friction between A and B is μ).
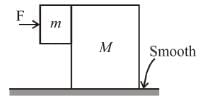
The two blocks, m = 10kg and M = 50kg are free to move as shown. The coefficient of static friction between the blocks is 0.5 and there is no friction between M and the ground. A minimum horizontal force F is applied to hold m against M that is equal to :
A given object takes n times more time to slide down 45° rough inclined plane as it takes to slide down a perfectly smooth 45° incline. The coefficient of kinetic friction between the objects and the incline is.
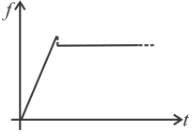
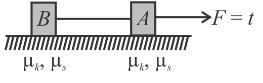
A force F = t is applied to a block A as shown in figure, where t is time in seconds. The force is applied at t = 0 seconds when the system was at rest. Which of the following graph correctly give the frictional force between A and horizontal surface as a function of time t. [Assume that at t = 0, tension in the string connecting the two blocks is zero].
Given mA = 20kg, mB = 10kg, mC = 20kg. Between A and B, µ1 = 0.3, between B and C, µ2 = 0.3 and between C and ground µ3 = 0.1. The least horizontal force F to start the motion of any part of the system of three blocks resting upon one another as shown in figure is (g = 10 m/s2)