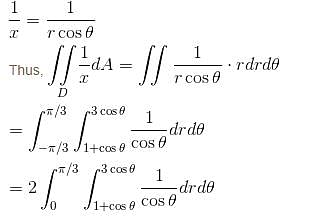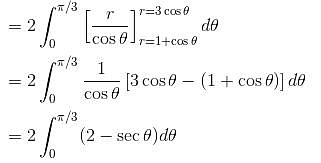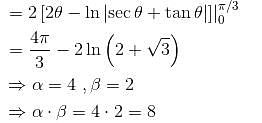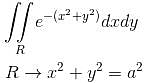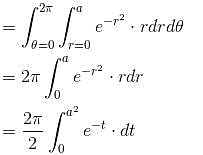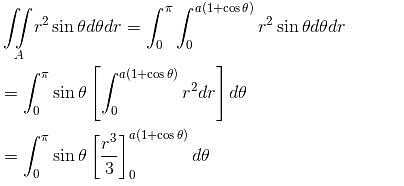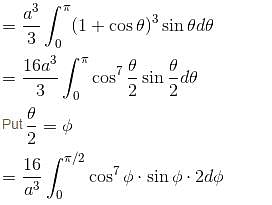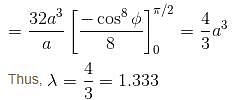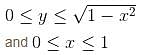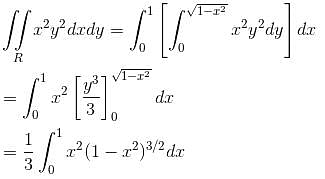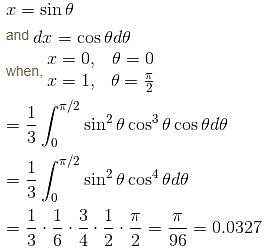Integral Calculus NAT Level - 1 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Integral Calculus NAT Level - 1
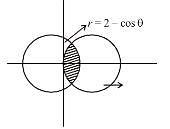
Find the area between the curves r = 3 cos θ and r = 2 - cos θ is απ + β√3. Find the value of α + β.
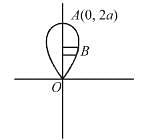
Find by Double Integration, whole area of the curve a2x2 = y3(2a – y). Let area be of the form λa2. Find value of λ.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Find the whole area included between the curve x2y2 = a2(y2 – x2) and its asymptotes. It is of form λa2. Find value of λ.
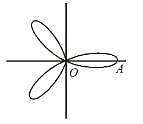
Find the area bounded by the curve r = 4cos3θ. as given below :

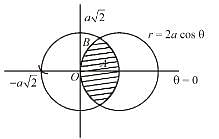
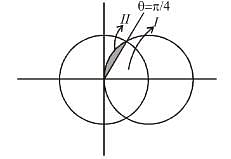
If the area common to the circles r = a√2 and r = 2a cosθ is a2λ. Find the value of λ.
The area bounded by the curve √x + √y = 1 and the coordinates axes is
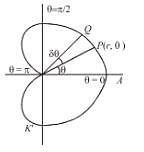
 where D is the region that lies inside the circle r = 3cosθ and outside the cadioid r = 1 + cos θ is
where D is the region that lies inside the circle r = 3cosθ and outside the cadioid r = 1 + cos θ is 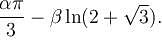 Find the value of α . β.
Find the value of α . β.
Find the value of 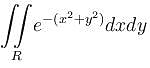 where R is a circular disk x2 + y2 = a2 is
where R is a circular disk x2 + y2 = a2 is 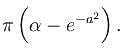 Find the value of α.
Find the value of α.
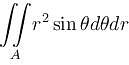 over the area of cardioid r = a(1 + cosθ) above initial line is λa3. Find the value of λ.
over the area of cardioid r = a(1 + cosθ) above initial line is λa3. Find the value of λ.
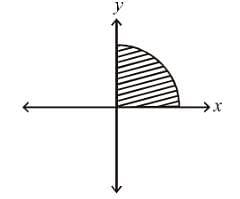
Evaluate  over the domain {{x, y) : x > 0, y > 0, x2 + y2 < 1}
over the domain {{x, y) : x > 0, y > 0, x2 + y2 < 1}



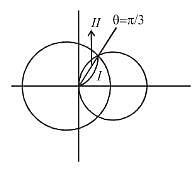
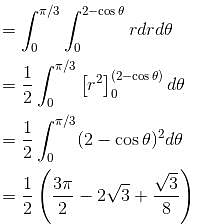

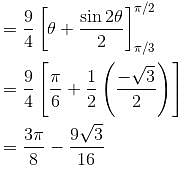
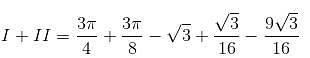
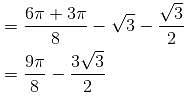
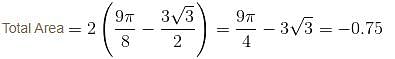
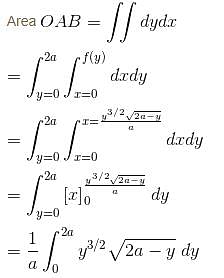
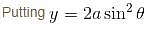

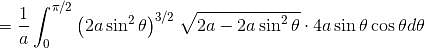
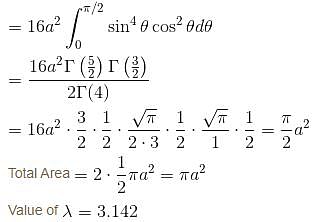

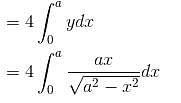
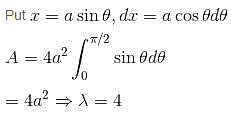
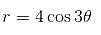
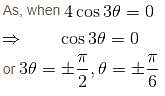
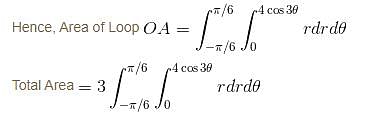
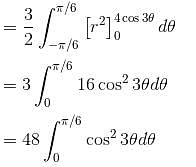
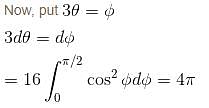
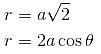

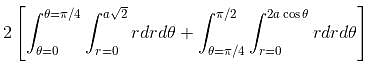
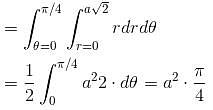
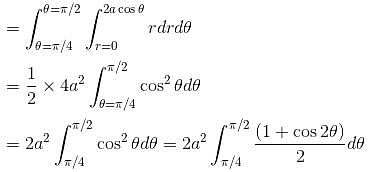
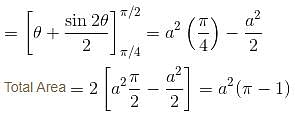
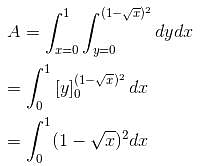
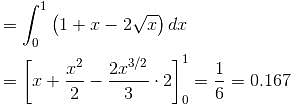
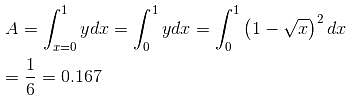
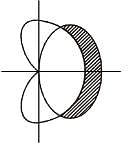

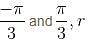 varies from 1 + cos θ (cardioid) to 3 cos θ (circle).
varies from 1 + cos θ (cardioid) to 3 cos θ (circle).