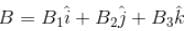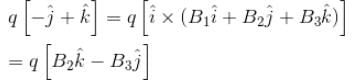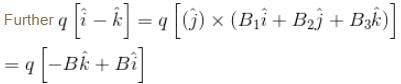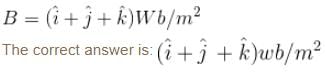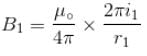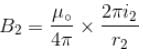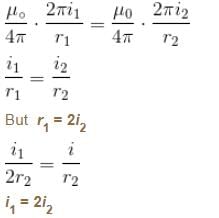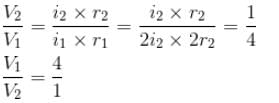Magnetostatics MCQ Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Magnetostatics MCQ Level - 2
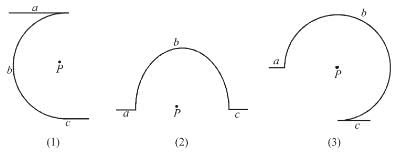
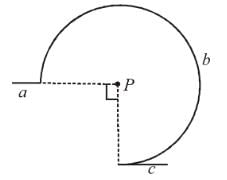
Figure here shows three close in all cases the circular path has radius r and straight ones are infinitely long. For same current the magnetic field at the centre P in cases 1, 2, 3 have the ratio :

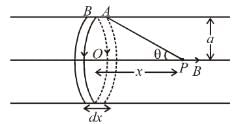
A disc of radius R rotates constant angular velocity ω about its own axis surface density of this disc varies as σ = αr2, where r is the distance from the centre of the disc. Determine the magnetic field intensity at the centre of disc.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
For a solenoid of length l, having N turns, the magnetic field at a point on its axis is given by :
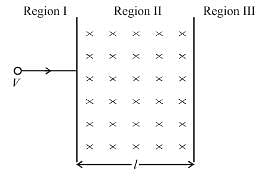
A particle of mass m and charge q, moving with velocity v enters region II normal to the boundary as shown in the figure. Region II has a uniform Magnetic field B perpendicular to the plane of he paper. The length of the Region II is l. Choose the incorrect choice(s)
The magnetic field at the centre of square of side a is :
A coil of 100 turns and area 2 × 10–2 m2 is pivoted about a vertical diameter in a uniform magnetic field and carries a current of 5A. When the coil is held with its plane in north south direction it experiences a couple of 0.33 Nm. When the plane is east-west, the corresponding couple is 0.4 Nm the value of magnetic induction is [Neglect earth’s magnetic field]
A wire of length L is bent in the form of a circular coil and current i is passed through it. If this coil is placed in a magnetic field then the torque acting on the coil will be maximum when the number of turns is :
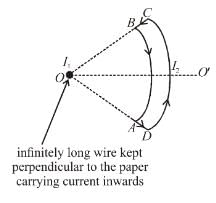
Which of the following statement is (are) correct in the given figure?
A charge q is moving with a velocity 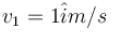 at a point in a magnetic field and experience a force
at a point in a magnetic field and experience a force 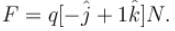 If the charge is moving with velocity
If the charge is moving with velocity 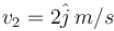 at the same point, it experience a force
at the same point, it experience a force
F2 = q(i - k)N The magnetic induction B at that point is :
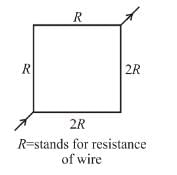
Two circular coil 1 and 2 are made from the same wire but the radius of the 1st coil is twice that of the 2nd coil. What is the ratio of potential difference applied across them, so that magnetic field at their centre is same ?



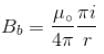
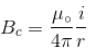
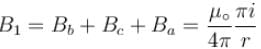
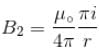
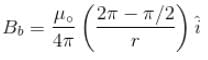
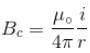
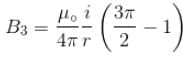
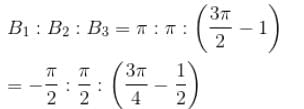
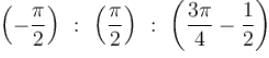
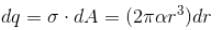
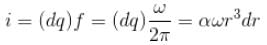
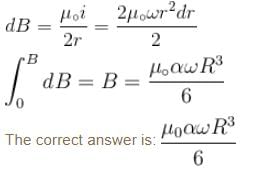
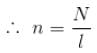
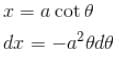
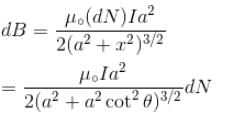
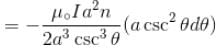
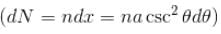
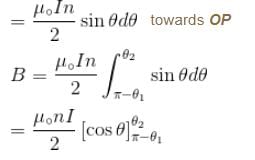
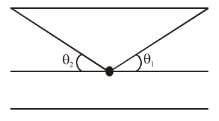
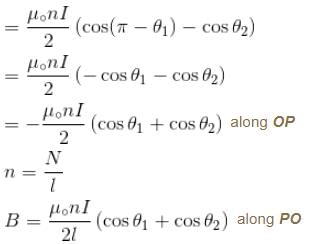
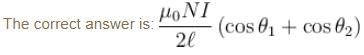
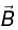 is perpendicular to velocity
is perpendicular to velocity 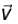 therefore, path of particle is circle is region II Particle enters in region III if, radius of circular path,
therefore, path of particle is circle is region II Particle enters in region III if, radius of circular path,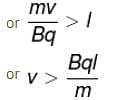
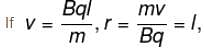 particle will turn back and path length will be maximum. If particle returns to region I, time spent in region II will be :
particle will turn back and path length will be maximum. If particle returns to region I, time spent in region II will be :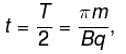 which is independent of V
which is independent of V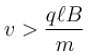
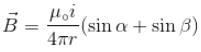 α and β are the angle
α and β are the angle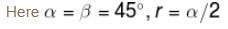
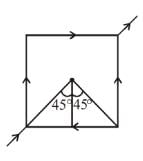
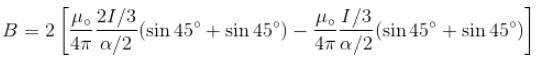
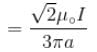
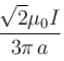
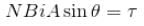
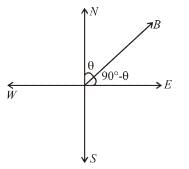
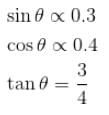
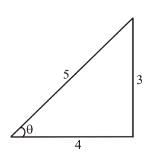
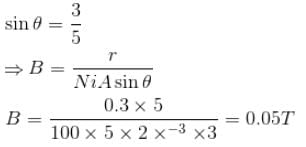
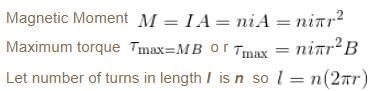
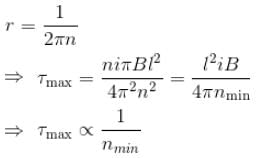
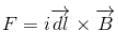
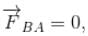 because magnetic line are parallel to this wire.
because magnetic line are parallel to this wire.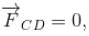
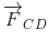 is perpendicular to paper outward and
is perpendicular to paper outward and 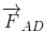 is perpendicular to paper inward. These two force (although calculated by integration) cancel each other but produce a torque which tend to relate the loop in clockwise direction about an axis OO'.
is perpendicular to paper inward. These two force (although calculated by integration) cancel each other but produce a torque which tend to relate the loop in clockwise direction about an axis OO'.