Linear Algebra MCQ Level - 1 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Linear Algebra MCQ Level - 1
Let A be a m × n matrix with row rank = r = column rank. The dimension of the space of solution of the system of linear equations AX = 0 is :
What would be the dimension for the general solution of the homogeneous system.
x1 + 2x2 – 3x3 + 2x4 – 4x5 = 0
2x1 + 4x2 – 5x3 + x4 – 6x5 = 0
5x1 + 10x2 – 13x3 + 4x4 – 16x5 = 0
2x1 + 4x2 – 5x3 + x4 – 6x5 = 0
5x1 + 10x2 – 13x3 + 4x4 – 16x5 = 0
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A matrix M has eigen values 1 and 4 with corresponding eigen vectors (1, –1)T and (2, 1)T, respectively. Then M is :
If rank of matrix A is 5 and nullity of A is 3, then A is of order :
The three equations,
–2x + y + z = a
x – 2y + z = b
x + y – 2z = c
will have no solution, unless :
The matrix A is represented as . The transpose of the matrix of this matrix is represented as?
Find the values of x, y, z and w from the below condition.
Let P be a matrix of order m × n and Q be a matrix of order n × p, n ≠ p. If rank (P) = n and rank of (Q) = p, then rank (PQ) is :


 – rank = n – r
– rank = n – r
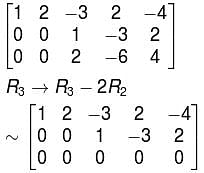
 then A-1 is equal to :
then A-1 is equal to :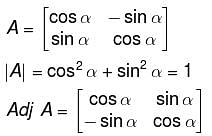



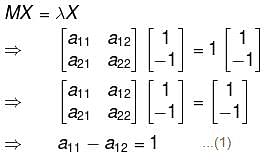

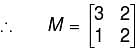
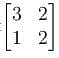
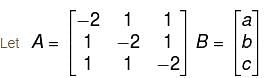
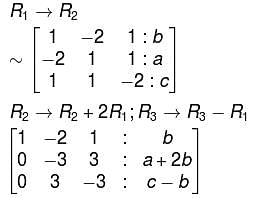
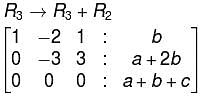
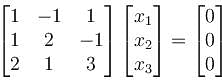 will give,
will give,















