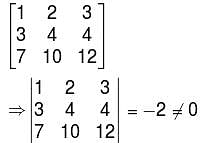Linear Algebra MCQ Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Linear Algebra MCQ Level - 2
The system of the equations,
x – 4y + 7z = 14
3x + 8y – 2z = 13
7x – 8y + 26z = 5
is :
x – 4y + 7z = 14
3x + 8y – 2z = 13
7x – 8y + 26z = 5
is :
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
For what values of k, the given system of equations will have a unique solution?
2x + 3ky + (3k + 4)z = 0
x + (k + 4)y + (4k + 2)z = 0
x + 2(k + 1)y + (3k + 4)z = 0
2x + 3ky + (3k + 4)z = 0
x + (k + 4)y + (4k + 2)z = 0
x + 2(k + 1)y + (3k + 4)z = 0
Which of the following will satisfy the given system?
2x1 – 3x2 – 6x3 – 5x4 + 2x5 = 7
x3 + 3x4 – 7x5 = 6
x4 – 2x5 = 1
The system of equations,
x + y + z = 0
2x – y – 3z = 0
3x – 5y + 4z = 0
x + 17y + 4z = 0
Will have :
Choose the correct option about the system,
3x + y + z = 8
–x + y – 2z = –5
x + y + z = 6
–2x + 2y – 3z = –7
A necessary and sufficient condition that values, not all zero may be assigned to n variables x1, x2, ......., xn so that the homogeneous equations, ai1x1 + ai2x2 + ..... + ainxn = 0 (i = 1, 2,.....n) hold simultaneously, is :
Consider the following statements about the given system of equations,
x + 2y + 3z = 0
3x + 4y + 4z = 0
7x + 10y + 12z = 0
and choose the correct one


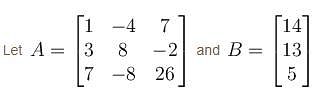

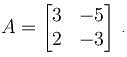 Then
Then
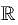 .Then t(t) has no real roots. Thus A has no eigenvalues and no eigen vectors.
.Then t(t) has no real roots. Thus A has no eigenvalues and no eigen vectors. .
. 
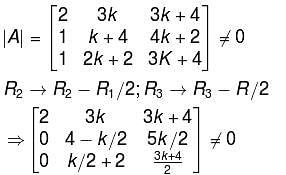
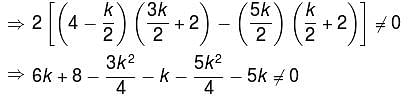
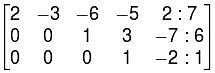

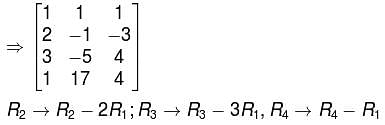
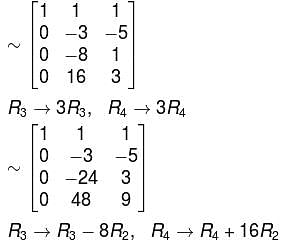

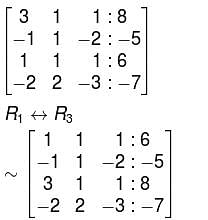
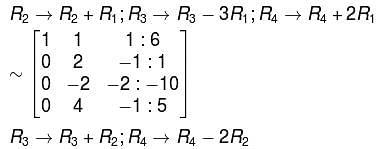
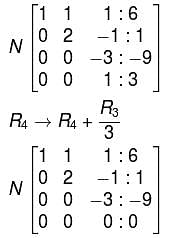
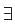 unique solution, the system reduces to,
unique solution, the system reduces to,