Olympiad Test: Area, Perimeter And Volume - Class 5 MCQ
20 Questions MCQ Test Math Olympiad for Class 5 - Olympiad Test: Area, Perimeter And Volume
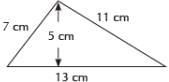
Find the perimeter of the triangle shown in the previous question.
Find the area of the parallelogram shown.


Find the perimeter of the parallelogram shown in the previous question.
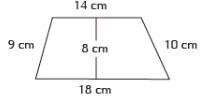
Find the perimeter of the trapezoid shown in the previous question.
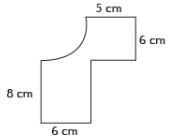
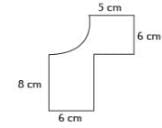
Find the perimeter of the figure shown in the below
A square has an area of 64 cm2. What is the length of each side?
The figure below is made up of 3 squares of sides 5 cm. What is the perimeter of the figure?
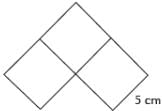
The figure below is made up of three squares. Find the perimeter of the figure.


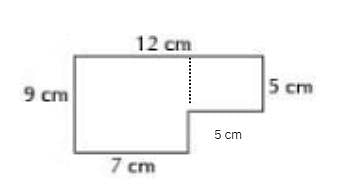
The area of the figure above is _____
m2.
The perimeter of a square is 20 cm. What is the length of each side of the square?
Which of the following figures have the same shaded area?

Which one of the following rectangles had the biggest perimeter?
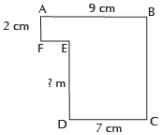
The perimeter of the figure shown below is 36 m. What is the length of DE?
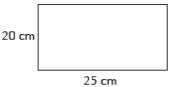
Calculate the area of rectangle if one square represents an area of 1 cm2 .

A rectangular garden measures 25 m by 20 m. What is the cost of erecting a wooden fence around it if every 5 metres of wooden fencing cost $ 27?
|
32 videos|57 docs|45 tests
|