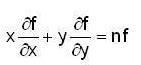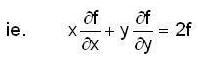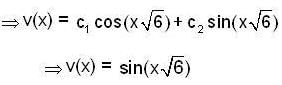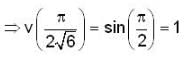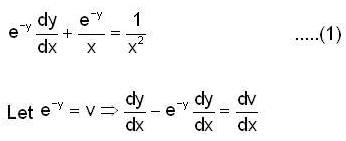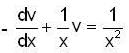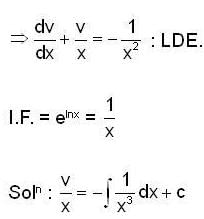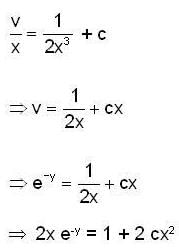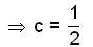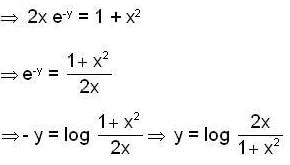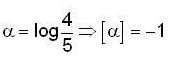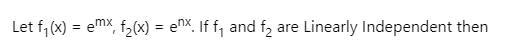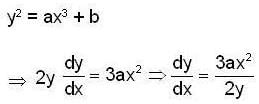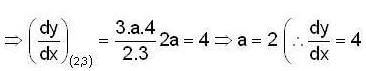IIT JAM Mathematics Practice Test- 2 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Practice Test- 2
Let 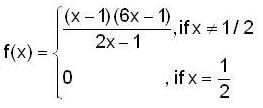 then at x = 1/2 , which of the following is/true ?
then at x = 1/2 , which of the following is/true ?
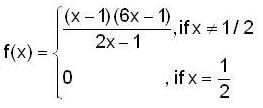 then at x = 1/2 , which of the following is/true ?
then at x = 1/2 , which of the following is/true ?The differential equation, 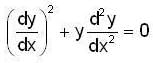 can be reduced to (where α is a constant)
can be reduced to (where α is a constant)
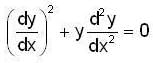 can be reduced to (where α is a constant)
can be reduced to (where α is a constant)The differential equation y" + (x3 sin x)5 y' + y = cos x3 is
If y1 (x) = x is a solution of differential 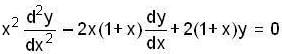 equation, then the second linearly independent solution is
equation, then the second linearly independent solution is
Given that y = x3 is one of the L.I. solution of the differential equation x2y2 + xy1 - 9y = 0, then the other L.I. solution i s ________ .
A cubic function f(x) vanishes at x = -2 and has maxima / minima at x = 1 /3 , x = -1 resp. 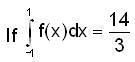 then f(x) is equal to
then f(x) is equal to
If a differential equation is given by xy1 - y = (x - 1) (y2 - x + 1), then one of the part of C.F. i s _______ .
Consider the boundary value problem
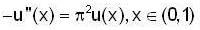
u(0) = u(1) = 0. If u and u1 are continuous on [ 0, 1 ], then which of the following is not true ?
Let y1 (x) and y2(x) form a complete set of solutions of the differential equation 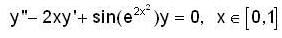 with y1(0) = 0, y‘1(0 ) = 1 ,y'2(0) = 1 and y2(0) = 1. If ω(x) is the wrenskian o f y1 and y2 , then ω(1) is
with y1(0) = 0, y‘1(0 ) = 1 ,y'2(0) = 1 and y2(0) = 1. If ω(x) is the wrenskian o f y1 and y2 , then ω(1) is
Consider the 2nd order Cauchy-Euler differential equation
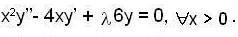
Then the values of λ for which all the solutions of above DE tends to 0 as x →∞ , is
Consider the two statements given below :
I) The curves y = ax3 and x2 + 3y2 = c2 form orthogonal Trajectories
II) The differential equation of the 2nd cuive (In I) is obtained from the differential equation of the first cuive (in I) by replacement of 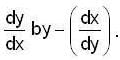
Then the correct answer is,
The orthogonal trejections of the family of parabola’s y2 = 4ax + 4a2 is the family
Let y(x) be the solution of the differential equation (x3 - 2y2) dx + 2xy dy = 0 Satisfying y(1) = 1, then which of the following is true ?
Let y(x) be the solution of the differential equation 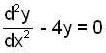 such that y(0) = 1 and y’(0) = β Then the values of β ∈ [0,21, such that the minimum of the set{y (x)/x∈ R } is greater than or equal to 2.
such that y(0) = 1 and y’(0) = β Then the values of β ∈ [0,21, such that the minimum of the set{y (x)/x∈ R } is greater than or equal to 2.
Consider the differential equation, 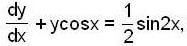 then which are true for this different equation,
then which are true for this different equation,
If f(x) , g(x) are twice differential functions on [ 0, 2 ] satisfying f"(x) = g "(x ), f (1) = 2 g’(1) = 4 and f(2) = 3, g(z) = g, then
If y1 = xm and y2 = xn. where m and n are constants, are two solutions of a 2nd order homogeneous linear differential equation with constant coefficient, then y = C1y1 + C2y2 be a solution if,
Consider the differential equation x2y" + 3xy' - λ= 0, then,
Which of the following(s) is/are not the solution of the differential equation y(xy + 2x2y2)dx + x(xy - x2y2)dy = 0 ?
If f(x) = ax2 + bx + c,then the value of G in the first mean value theorem f(x + h) - f(x) = h f (x + θh) i s _________ .
if 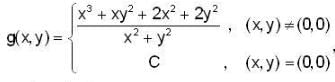 lf g is continuous at (0,0) then the value of c is ___________.
lf g is continuous at (0,0) then the value of c is ___________.
If u = log (tan x + tan y) then the value of 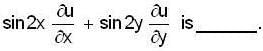
Let y(x) = v(x) secx, be the solution of initial value problem,
y" - 2y tanx + 5y = 0 with y(0) = o ,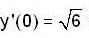 then
then 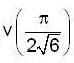 is equal to_______.
is equal to_______.
If (c1 + c2 In x) /x is the general solution of the differential equation x > 0, then k equals
If an integral cuive of the differential equation 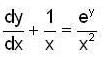
passes through the point (1,0) and 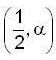
then the value of [a] is _______________ (where [.] denotes greatest integer function).
If the equation of the tangent to the curre y2 = ax3 + b at the point (2,3) is y = 4x - 5 then the value of a + b is ________.


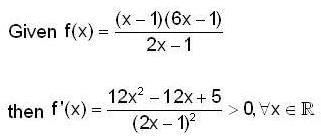
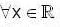

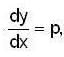 therefore
therefore 
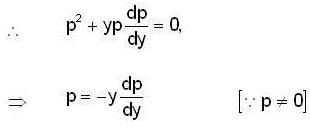
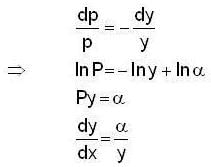

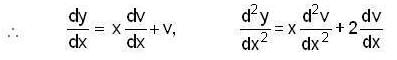
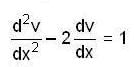 ..(1)
..(1)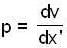 then (1) gives
then (1) gives 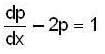
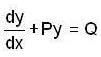 whose
whose 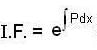 then
then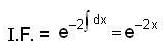
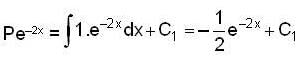
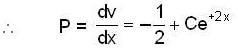
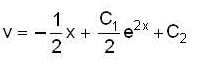
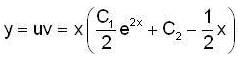
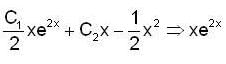
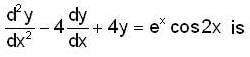
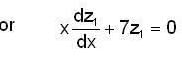
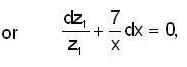

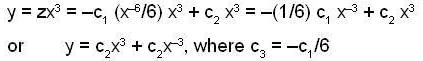
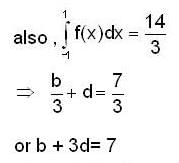
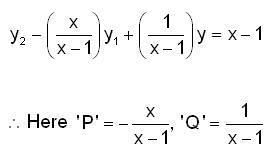

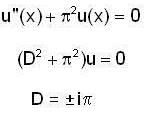
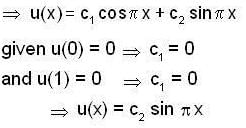
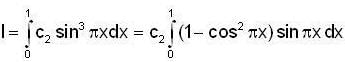
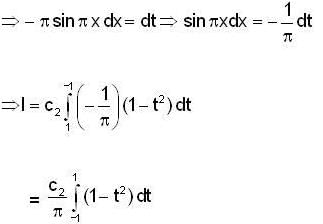
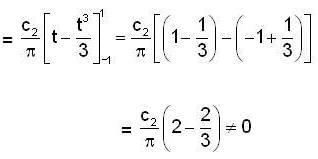
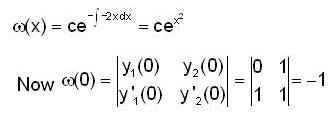

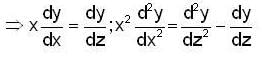
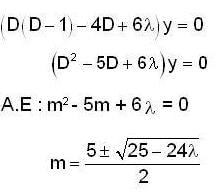
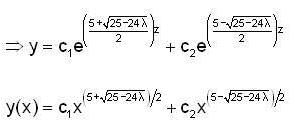
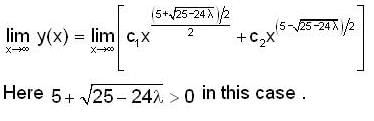
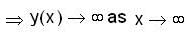
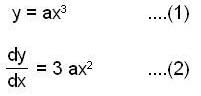
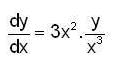
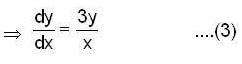
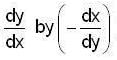 in (3) we have
in (3) we have
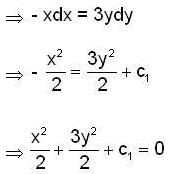

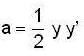 put it in (1), we have
put it in (1), we have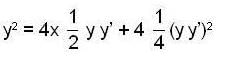
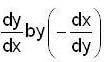 in (2) , to get the DE. of orthogonal trajectories,
in (2) , to get the DE. of orthogonal trajectories,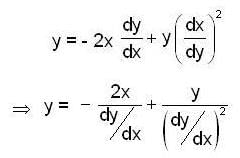
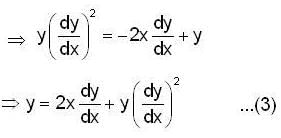 which is the same as the differential equation (2) of the given system (1). Hence the system of parabolas (1) is self orthogonal i.e. each member of the given family of parabola's intersects its own member orthogonally.
which is the same as the differential equation (2) of the given system (1). Hence the system of parabolas (1) is self orthogonal i.e. each member of the given family of parabola's intersects its own member orthogonally.
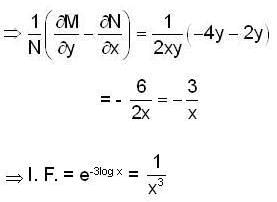
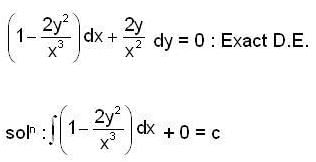
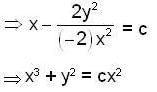
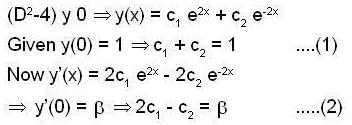
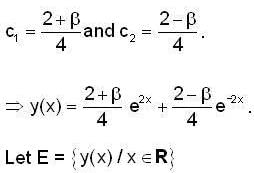
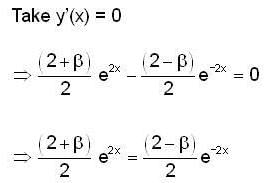
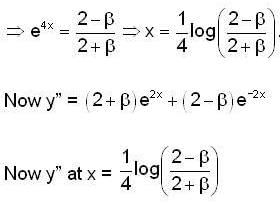
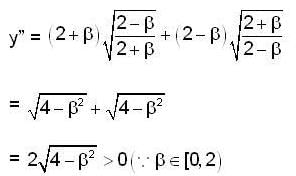
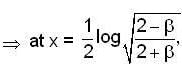 E has minimum value .
E has minimum value . 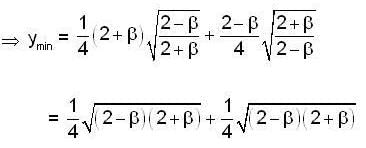
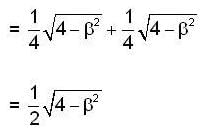
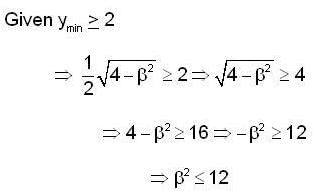
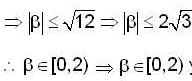

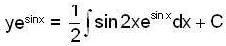

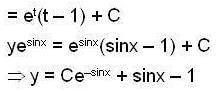
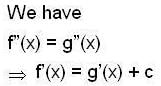
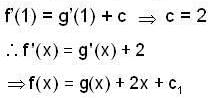
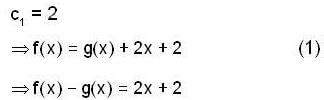
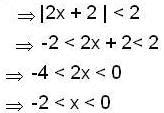
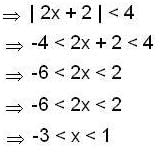
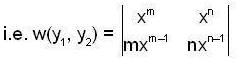
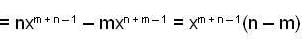
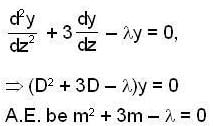
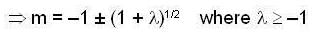
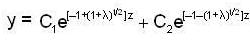
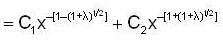
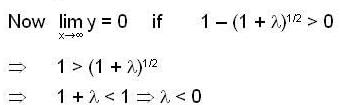
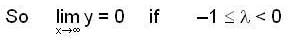
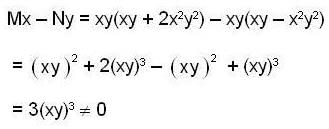
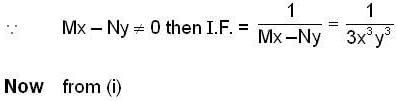
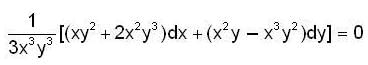
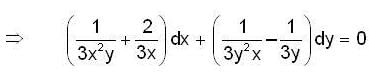

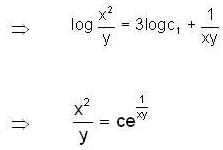
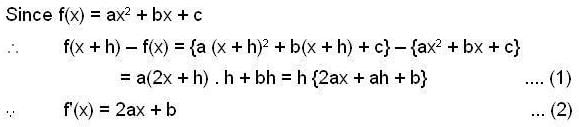
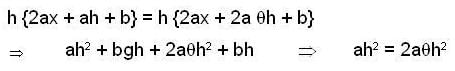

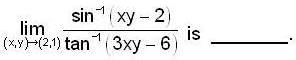
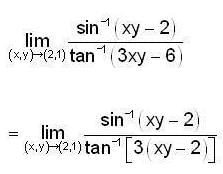

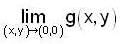
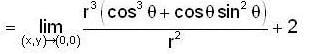
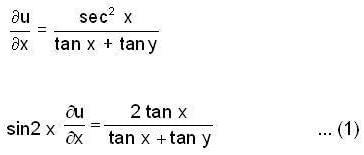
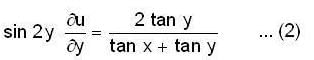
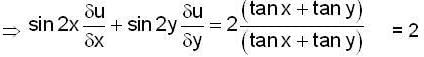
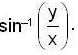 Then
Then 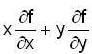 is equal to ______.
is equal to ______.