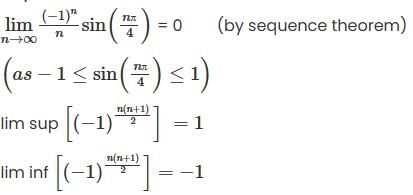IIT JAM Mathematics Mock Test- 4 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Mock Test- 4
The orthogonal trajectories of the family of curves y = c1x3, where c1 is arbitary costant, is
Suppose f ; ℝ→ℝ is an odd and differentiable fraction. Then for every x0 ∈ ℝ. f'(-x0) is equal to;
Let  denote the eigenvalues of the matrix
denote the eigenvalues of the matrix 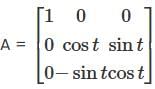
If  , then the set of possible values of t, -π ≤ t < π, is
, then the set of possible values of t, -π ≤ t < π, is
 denote the eigenvalues of the matrix
denote the eigenvalues of the matrix 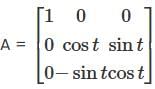
 , then the set of possible values of t, -π ≤ t < π, is
, then the set of possible values of t, -π ≤ t < π, isf T = 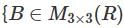 | eigen values of B are in Z}, then which of the following statement(s) is true?
| eigen values of B are in Z}, then which of the following statement(s) is true?
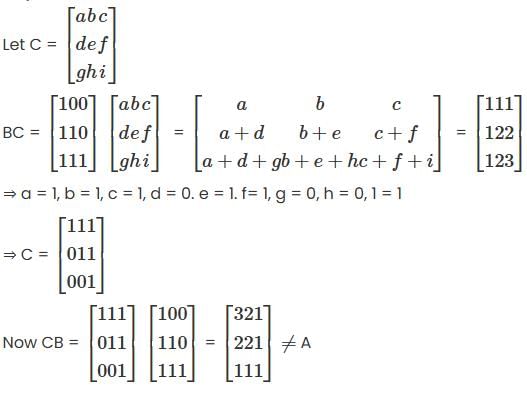
Let T = {B ∈ M3 x 3(ℝ) | eigenvalues of B are integers}. Which of the following statements is/are true?
Number of elements of order p in Zp2q where p and q are distinct prime is;
An object moves in the force field 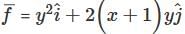 How much work is performed on the object moves from (2, 0) counter clockwise along the elliptical path x2 +4y2 = 4 to (0. 1), then back to (2,0) along the line segment joining the two points.
How much work is performed on the object moves from (2, 0) counter clockwise along the elliptical path x2 +4y2 = 4 to (0. 1), then back to (2,0) along the line segment joining the two points.
The area bounded by x2 + y2 = 25, 4y = |4 - ��2| and x = 0 in the first quadrant is 
Then k is
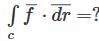 where
where  and 'c' be the quarter circular path x2 + y2 = a2 from (a, 0) to (0, a)
and 'c' be the quarter circular path x2 + y2 = a2 from (a, 0) to (0, a)
Let σ be the 12- cycles (1 2 3 4 5 6 7 8 9 10 11 12) for which positive integer i is σi also a 12 cycle?
If R→R is given by f(x) = x3 + x2f'(1) + xf''(2) + f'''(3) for all x in R. then f(2) - f(1) is
Let 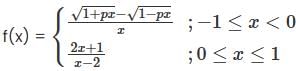 . If f(x) is continuous in the interval [-1, 1], then p equals
. If f(x) is continuous in the interval [-1, 1], then p equals
If x3y2 is an integrating factor of (6y2 + axy)dx + (6xy + bx2)dy =0, a, b ∈ ℝ then
The radius of convergence of the series 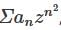 , where a0 = 1. an = 3-n an-1 for n ∈ ℕ, is
, where a0 = 1. an = 3-n an-1 for n ∈ ℕ, is
Let 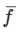 be a smooth vector function of a real variable. Consder two statements
be a smooth vector function of a real variable. Consder two statements
S1 div curl 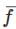 = 0
= 0
S2; grad div  = 0
= 0
Then
Let G be the group with the generators a and b given byG = {(a,b)|σ(a) = 4,σ(b) = 2, ba = a-1b}. Let Z(G) denotes the centre of G. Then G/Z(G) is isomorphic to.
Suppose that L(y) = y'' + a1y' + a2y = b(x), where a1, a2 are constants and b(x) is a continuous function on 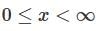 Then consider the statements
Then consider the statements
I. If b(x) is bounded on [0, ∞), then every solution of L(y) = b(x) is bounded on [0, ∞).
II. If b(x) → 0 as x → ∞, then every solution of L(y) = b(x) tends too as x → ∞.
Let y(x) be a non-trivial solution of the second order linear differential equation
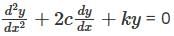
where c < 0. k > 0 and C2 > k , then
Let P1, P2 and P3 denote. respectively, the planes defined by
a1x+b1y+c1z= = α1
a2x + b2y+c2z= α2
a3x-b3y + c3z = α3
It is given that P1, P2, P3 intersect exactly at one point when α1 = α2 = α3 = 1, If now
α1 = 2, α2 = 3 and α3 = 4 then the planes


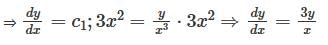



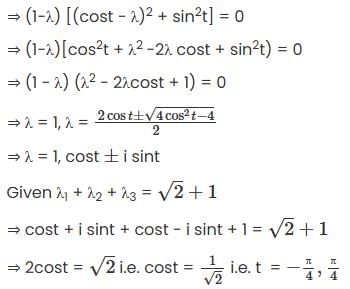
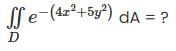
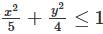 is
is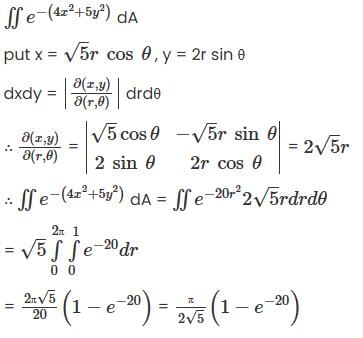
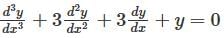 is
is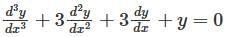
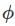 (d).
(d).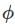 (p) = p-1
(p) = p-1
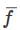 is independent of path
is independent of path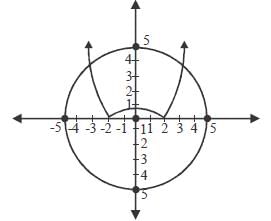
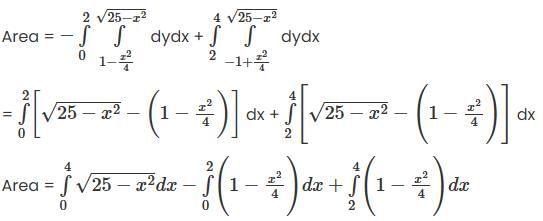

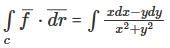
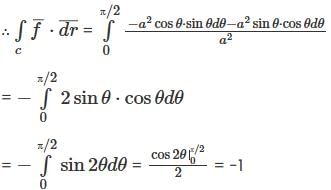
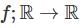
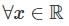
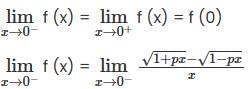
 here f is continuous over [0, 1], so f(x) is uniformly continuous.
here f is continuous over [0, 1], so f(x) is uniformly continuous.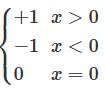
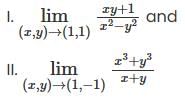
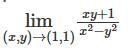
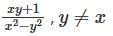
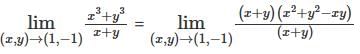
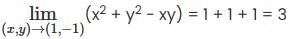
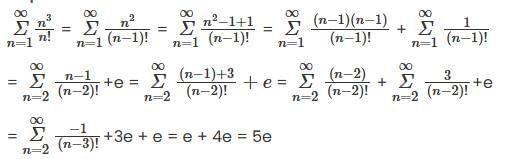
 converges and sum is 5e.
converges and sum is 5e.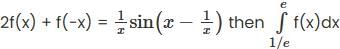 is
is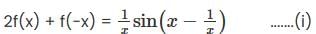
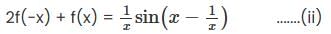
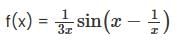
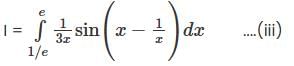
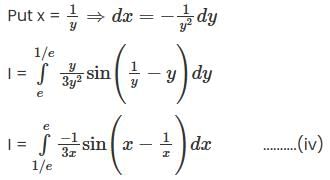
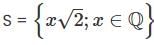 then the closure of S is
then the closure of S is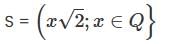
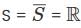 Which is uncountable
Which is uncountable
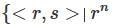 = 1,s2 = 1, rs = sr2} then
= 1,s2 = 1, rs = sr2} then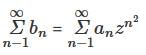
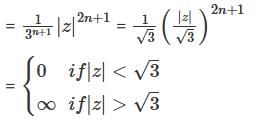
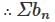 convergent if |z| < √3 and divergent if |z| > √3
convergent if |z| < √3 and divergent if |z| > √3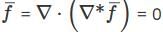 ⇒ S1 is true
⇒ S1 is true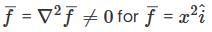
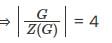
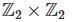
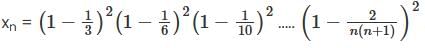 . n>2. Then lim(xn) is;
. n>2. Then lim(xn) is;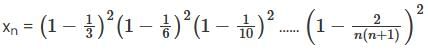
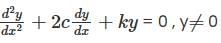
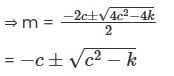
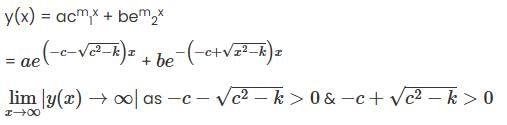
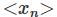 where
where  . Then
. Then 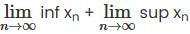 is
is