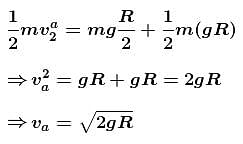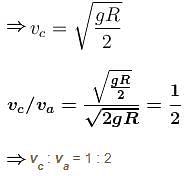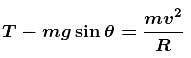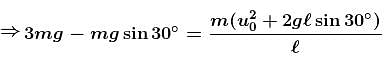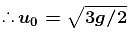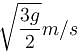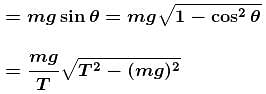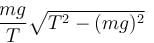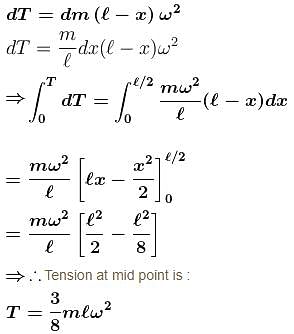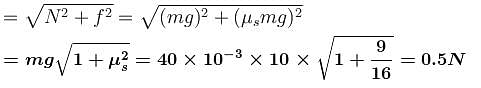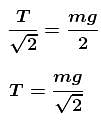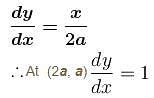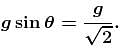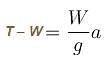Circular Motion MCQ Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Circular Motion MCQ Level - 2
A particle initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B. C is centre of the hemisphere. The equation relating α and β is :
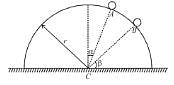

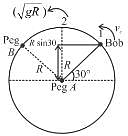
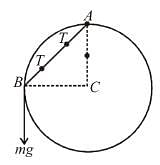
A bob is attached to one end of a string other end of which is fixed at peg A. The bob is taken to a position where string makes an angle of 30° with the horizontal. On the circular path of the bob in vertical plane there is a peg ‘B’ at a symmetrical position with respect to the position of release as shown in the figure. If vc and va be the minimum speeds in clockwise and anticlockwise directions respectively, given to the bob in order to hit the peg ‘B’ then ratio vc : va is equal to :

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
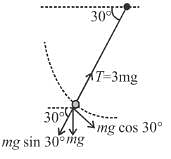
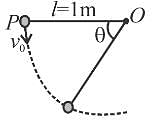
The sphere at P is given a downward velocity v0 and swings in a vertical plane at the end of a rope of l = 1m attached to a support at O. The rope breaks at angle 30° from horizontal, knowing that it can withstand a maximum tension equal to three times the weight of the sphere. Then the value of v0 will be : (g = π2 m/s)

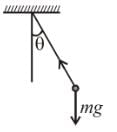
A simple pendulum is oscillating in a vertical plane. If resultant acceleration of bob of mass m at a point A is in horizontal direction, find the tangential force at this point in terms of tension T and mg.
A uniform rod of mass m and length l is rotating with constant angular velocity ω about an axis which passes through its one end and perpendicular to the length of rod. The area of cross section of the rod is A and its Young’s modulus is Y. Neglect gravity. The strain at the mid point of the rod is :
A small coin of mass 40 g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α = 2 rad/s2. The coefficient of static friction between the coin and the disc is µs = 3/4 and coefficient of kinetic friction µk = 0.5. The coin is placed at a distance r = 1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is :
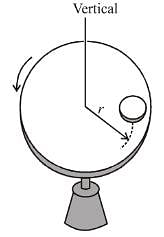
Objects A and B each of mass are connected by light inextensible cord. They are constrained to move on a frictionless ring in a vertical plane as shown in figure. The objects are released from rest at the positions shown. The tension in the cord just after release will be :
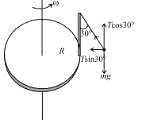
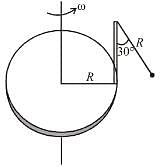
A disc of radius R has a light pole fixed perpendicular to the disc at the circumference which in turn has a pendulum of length R attached to its other end as shown in figure. The disc is rotated with a constant angular velocity ω. The string is making an angle 30° with the rod. Then the angular velocity ω of disc is :
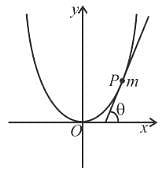
A bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equation is x2 = 4ay. The wire frame is fixed and the bead can slide on it without friction. The bead is released from the point y = 4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y = a is :

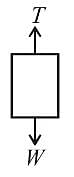
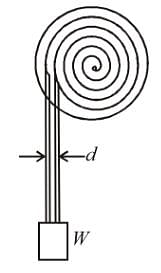
A weight W attached to the end of a flexible rope of diameter d = 0.75 cm is raised vertically by winding the rope on a reel as shown. If the reel is turned uniformly at the rate of 2 r.p.s. What is the tension in rope. The inertia of rope may be neglected.


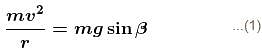
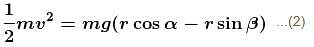
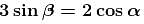
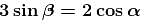
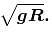 Conserving energy at (1) and (2) :
Conserving energy at (1) and (2) :