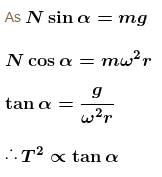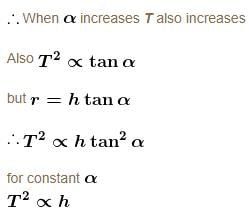Circular Motion MSQ - Physics MCQ
10 Questions MCQ Test - Circular Motion MSQ
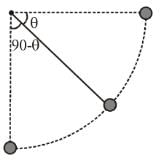
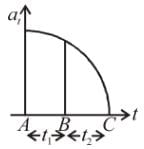
One end of a light string of length L is connected to a ball and the other end is connected to a fixed point O. The ball is released from rest at t = 0 with string horizontal and just taut. The ball then moves in vertical circular path as shown. The time taken by ball to go from position A to B is t1 and from B to lowest position C is t2. Let the velocity of ball at B is 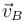 and at C is
and at C is 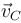 respectively. If
respectively. If 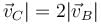 then, which of the following is true.
then, which of the following is true.
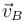 and at C is
and at C is 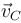 respectively. If
respectively. If 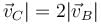 then, which of the following is true.
then, which of the following is true.
A machine, in an amusement park, consists of a cage at the end of one arm, hinged at O. The cage revolves along a vertical circle of radius r (ABCDEFGH) about its hinge O, at constant linear speed 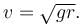 The cage is so attached that the man of weight ‘w’ standing on a weighing machine, inside the cage, is always vertical. Then which of the following is/are correct.
The cage is so attached that the man of weight ‘w’ standing on a weighing machine, inside the cage, is always vertical. Then which of the following is/are correct.
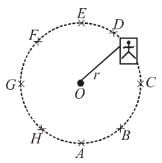
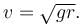 The cage is so attached that the man of weight ‘w’ standing on a weighing machine, inside the cage, is always vertical. Then which of the following is/are correct.
The cage is so attached that the man of weight ‘w’ standing on a weighing machine, inside the cage, is always vertical. Then which of the following is/are correct.
A particle is moving in a circular path. The acceleration and momentum vectors at an instant of time are 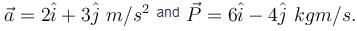 Then which of the following statement is incorrect
Then which of the following statement is incorrect
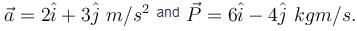 Then which of the following statement is incorrect
Then which of the following statement is incorrectA car driver going at some speed suddenly finds a wide wall at a distance r. To avoid hitting the wall he should.
Two particles A and B separated by a distance 2R are moving counter clockwise along the same circular path of radius R each with uniform speed v. At time t = 0. A is given a tangential acceleration of magnitude 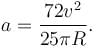
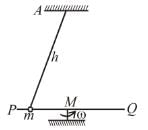
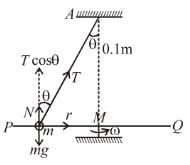
A smooth rod PQ rotates in a horizontal plane about its mid point M which is h = 0.1 m vertically below a fixed point A at a constant angular velocity 14 rad/s. A light elastic string of natural length 0.1 m force constant 1.47 N/cm has one end fixed at A and its other end attached to a ring of mass m = 0.3 kg which is free to slide along the rod. When the ring is stationary relative to rod, then which of following is correct.
On a circular table, A and B are moving on the circumference. Man A runs behind man B to catch him A runs with constant angular speed ω1 with respect to table and B runs at constant tangential speed v2 with respect to ground. If it is found that the table rotates 30° in the opposite direction in every one second and the initial angular separation between A and B is 30°, then A catches B after : (Radius of table is 3 m).
A small sphere of mass m suspended by a thread is first taken aside so that the thread forms the right angle with the vertical and then released, then :
A section of fixed smooth circular track of radius 20 m, in vertical plane is shown in the figure. A block is released from position A and leaves the track at B :
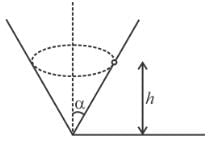
A particle is describing circular motion in a horizontal plane in contact with the smooth inside surface of a fixed right circular cone with its axis vertical and vertex down. The height of the plane of motion above the vertex is h and the semi-vertical angle of the cone is α. The period of revolution of the particle :


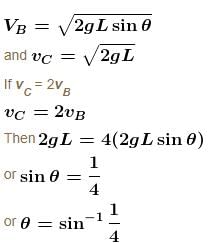
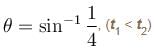
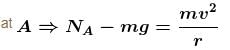 Put v ∴ NA – mg = mg
Put v ∴ NA – mg = mg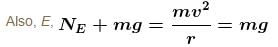
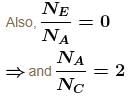



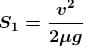
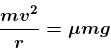

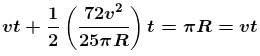
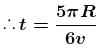
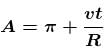
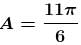
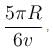 the angle covered of A is 11π/6
the angle covered of A is 11π/6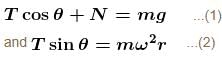
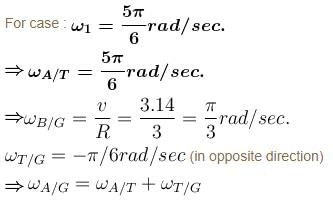

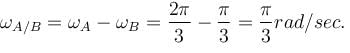

 A can not catch B within 0.5 sec
A can not catch B within 0.5 sec 
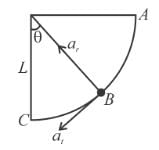

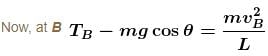
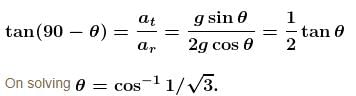
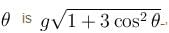 thread tension as a function of θ is T = 3mg cos θ between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontal is
thread tension as a function of θ is T = 3mg cos θ between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontal is 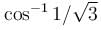
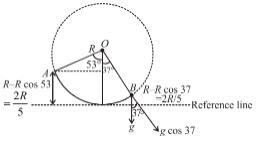
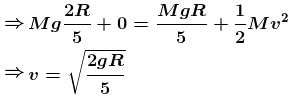

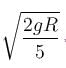 Radius of curvature of trajectory when leaves point B is R/2
Radius of curvature of trajectory when leaves point B is R/2