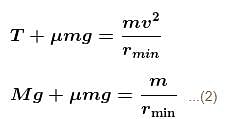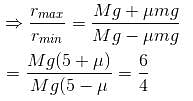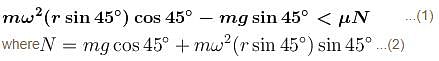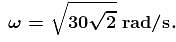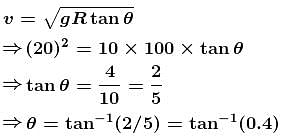Circular Motion NAT Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Circular Motion NAT Level - 2
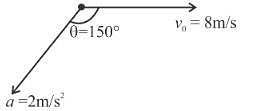
A ball is projected making and angle θ with the vertical. Consider a small part of the trajectory near the highest position and take it approximately to be a circular arc. What is the radius of this circle? This radius is called the radius of curvature (ROC) of the curve at the point if u = 20 then ROC in m.
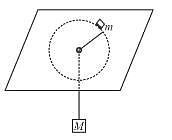
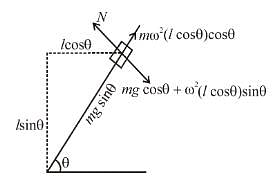
A small wedge whose base is horizontal is fixed to a vertical rod as shown in the figure 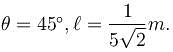 The slopping side of the wedge is frictionless and the wedge is spun with a constant angular speed ω about vertical axis as shown in the figure. Find
The slopping side of the wedge is frictionless and the wedge is spun with a constant angular speed ω about vertical axis as shown in the figure. Find
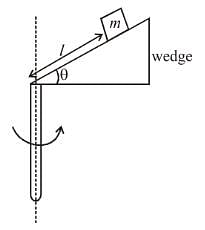
The value of angular speed ω (rad/sec) for which the block of mass m just does not slide down the wedge?
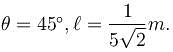 The slopping side of the wedge is frictionless and the wedge is spun with a constant angular speed ω about vertical axis as shown in the figure. Find
The slopping side of the wedge is frictionless and the wedge is spun with a constant angular speed ω about vertical axis as shown in the figure. Find
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
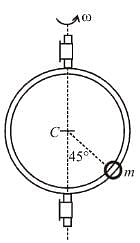
The member OA rotates about a horizontal axis through O with a constant counter clockwise velocity ω = 3 rad/sec. As it passes the position θ = 0, a small mass m is placed upon it at a radial distance r = 0.5m. If the mass is observed to slip at θ = 37°, the coefficient of friction between the mass and the member is ____ .
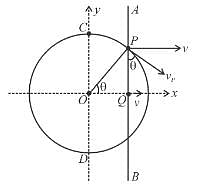
A rod AB is moving on a fixed circle of radius R with constant velocity ‘v’ as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x = 3R/5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
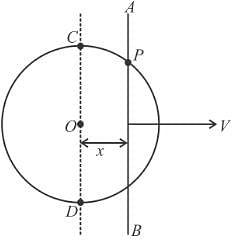
The speed of point of intersection P is 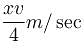 then x is
then x is
A squirrel climbing up a cylindrical post spirally makes the circle in a vertical height of four feet. If the top of the post is sixteen feet high and three feet in circumference, the distance travelled by it to reach the top is x in feet. Find the value of x/10
The figure shows the velocity and acceleration of a point like body at the initial moment of its motion. The acceleration vector of the body remains constant. The minimum radius of curvature of trajectory of the body is (in m.)
A ring of mass 2π kg and of radius 0.25m is making 300 -rpm about an axis through its centre perpendicular to its plane. The tension (in newtons) developed in the ring is :
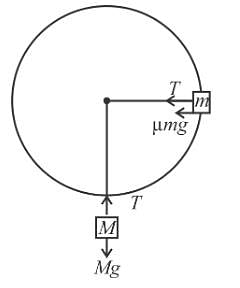
A toy car of mass m can travel at a fixed speed. It moves in a circle on a fixed horizontal table. A string is connected to car and attached to a block of mass M = 5m that hangs as shown in figure (the portion of string below the table is always vertical). The coefficient of friction between the surface of table and tyres of the toy car is µ = 1. The ratio of the maximum radius to the minimum radius for which the toy car can move in a circular path with centre O on table is x/4, then x is:
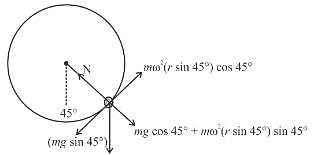
A small bead of mass m = 1 kg is carried by a circular hoop having centre at C and radius r = 1m which rotates about a fixed vertical axis (as shown). The coefficient of friction between bead and hoop is µ = 0.5. The maximum angular speed of the hoop for which the bead does not have relative motion with respect to hoop is given by (n√2)1/2.
A circular curve of a highway is designed for traffic moving at 72 km/h. If the radius of the curved path is 100m, the correct angle of banking of the road should be given by :n tan-1(n). Find the value of nAnswer



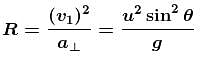
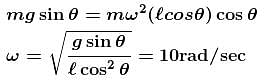
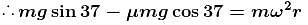
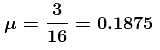
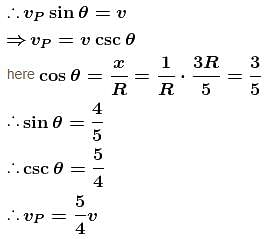
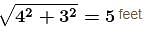
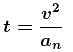
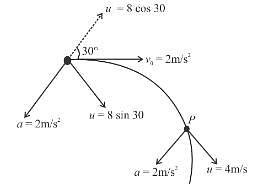
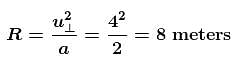
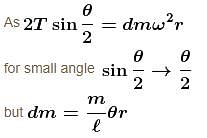
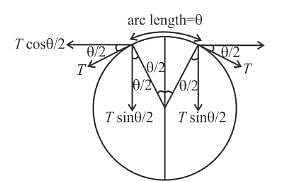
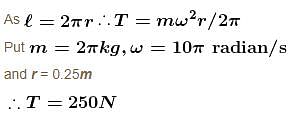
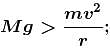 hence friction force on car of mass m will be outwards from the centre.
hence friction force on car of mass m will be outwards from the centre.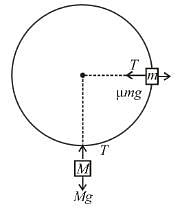
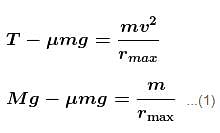
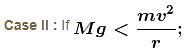 hence friction force on the car of mass m will be towards centre.
hence friction force on the car of mass m will be towards centre.