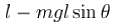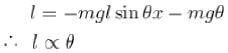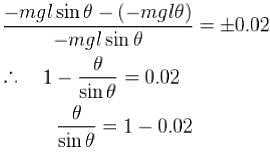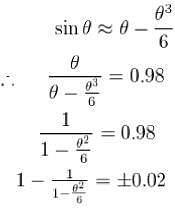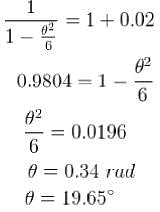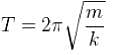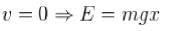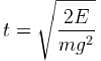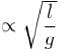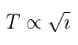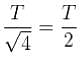Simple Harmonic Motion NAT Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Simple Harmonic Motion NAT Level - 2
A particle of mass m moves in one dimensional potential v(x)=-ax2 + bx4 where a and b are positive constants. What is the angular frequency of small oscillations about the minimum of the potential in units of 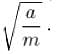
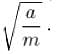
A spring of force constant k is stretched a certain distance. It takes twice as much work to stretch a second spring by half this distance. What is the force constant of the second spring? (in units of k)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
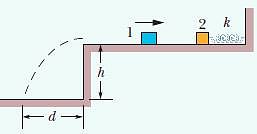
Above figure, shows block 1 of mass 0.200 kg sliding to the right over a frictionless elevated surface at a speed of 8.00 m/s. The block undergoes an elastic collision with stationary block 2, which is attached to a spring of spring constant 1208.5N/m. (Assume that the spring does not affect the collision.) After the collision, block 2 oscillates in SHM with a period of 0.140s, and block 1 slides off the opposite end of the elevated surface,landing a distanced from the base of that surface after falling height ℎ=4.90m. What is the value of d ?

What is the period of oscillation of a physical pendulum which consists of a circular hoop hanging from a nail an a wall the mass of the hoop is 3 kg and its radius is 20 cm, if it displaced slightly by a passing breeze? (in seconds)
A long straight and massless rod pivots about one end in a vertical plane. In configuration I, two small identical masses are attached to the free end, in the second configuration one mass is attached at the centre and the other is attached to the free end. What is the ratio of frequency of small oscillations of configuration / to that of configuration II?
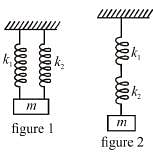
Two identical springs with spring constant k are connected to identical masses of mass in, as shown in the figures below the ratio of the period for the springs connected in parallel (figure I) to the period for the springs connected in series (figure 2) is what?
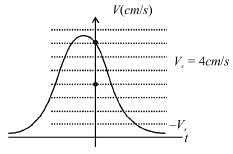
What is the phase constant in degrees for the harmonic oscillator with the velocity function V(f) given in figure if the position function x(t) has the form 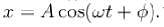 The vertical axis scale is set by Vs = 4 cm /s
The vertical axis scale is set by Vs = 4 cm /s
For a simple pendulum, find the angular displacement at which the restoring torque required for simple harmonic motion deviates from the actual restoring torque by 2% use g = 10m/s2 . (θ in degrees).
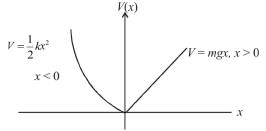
A particle of mass m moves in the potential shown above find the period of the motion when the particle has energy E. (in terms of 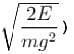
The circular hoops, X & Y are hanging on nails in a wall. The mass of X is four times of Yand the diameter of X is also four times that of Y and the diameter of X is also four times that of Y. If the period of small oscillations of Xis T, then find the period of oscillations for Y (in terms T)



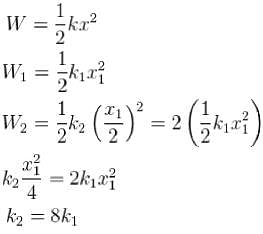
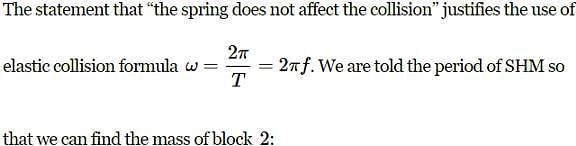
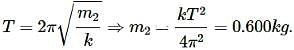
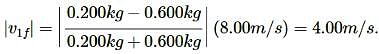

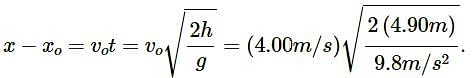
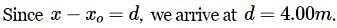
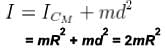


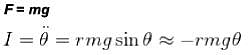




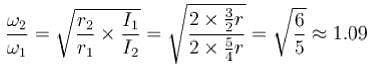
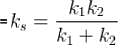
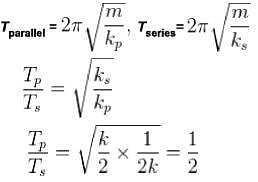
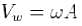 where → amplitude of oscillator
where → amplitude of oscillator 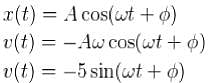
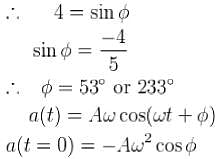
 ,acceleration would be positive but from the graph since the v is decreasing at
,acceleration would be positive but from the graph since the v is decreasing at