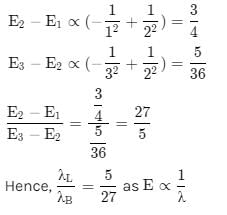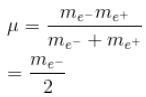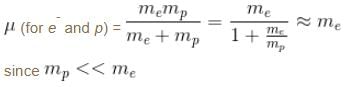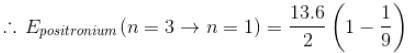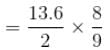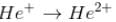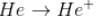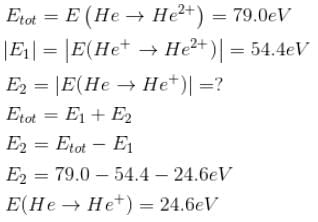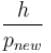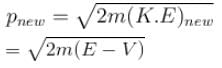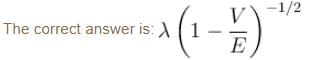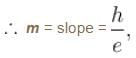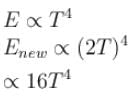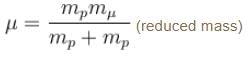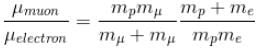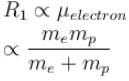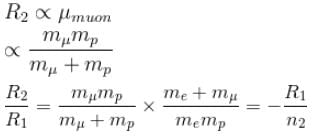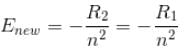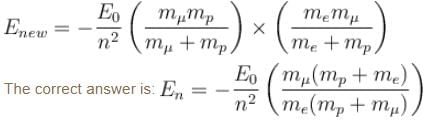Origin Of Quantum Mechanics MCQ Level - 2 - Physics MCQ
10 Questions MCQ Test Topic wise Tests for IIT JAM Physics - Origin Of Quantum Mechanics MCQ Level - 2
An atom has n = 1 and n = 2 levels filled. How many electrons does the atom have?
In a hydrogen atom, the ratio of the wavelengths of lyman-α radiation (in n = 2 to n =1) to Balmer-α radiation (n = 3 → n = 2) is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
de-Broglie hypothesized that the momentum and wavelength of a free massive particle are related by
Which of the following is true? When metallic surface is irradiated with white light
Positronium is an atom formed by an electron and a positron (anti electron), it is similar to the hydrogen atom with proton being replaced by a positron. If this positronium atom makes a transition from n = 3 to n = 1 the corresponding photon energy would be :
The energy required to remove both electrons from the helium atom in its ground state is 79.0 eV. How much energy is required to ionize helium? (i.e. to remove single electron)
A particle with initial K.E = E and de-Broglie wavelength λ enters a region in which it has potential energy V. What is the particle’s new de-Broglie wavelength?
In an experimental observation of the photoelectric effect, the stopping potential was plotted against the frequency of the incident light. Which of the following is the slope of the line?
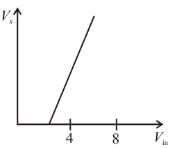
Here h is the planck's constant and φ is the work function of the metal
The energy from electromagnetic waves in equilibrium in a cavity is used to melt ice. If the temperature of the cavity is raised from T to 2T (in kelvin), then the mass of ice that can be melted increases by a factor of
If we replaced the electron in a hydrogen atom with muon, (mass of a neon is 207 times the mass of an electron) then what will be the energy levels En of this new hydrogen atom in terms of the binding energy E0 (of the ordinary hydrogen), mass of the proton mp and the principal quantum number, n? (mµ = 207 me)