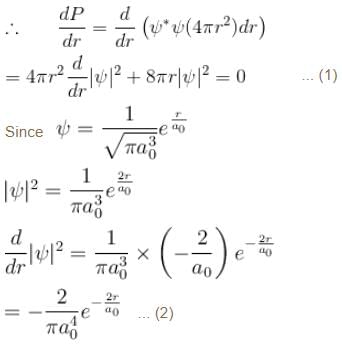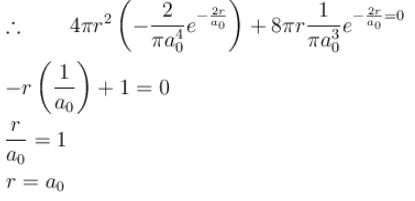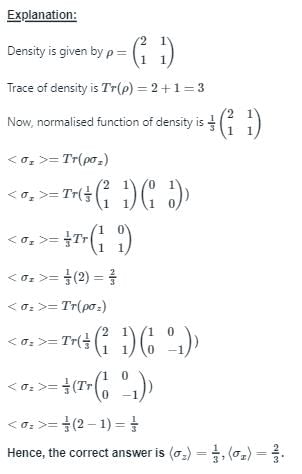Postulates Of Quantum Mechanics NAT - Physics MCQ
10 Questions MCQ Test - Postulates Of Quantum Mechanics NAT
The wave function 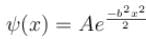 where A and B are real constant, is a normalised eigenfunction of the Schrödinger equation for a particle of mass M and energy E in a one dimensional potential V(x) such that V(x) = 0 at x = 0. Find the value for V in units of
where A and B are real constant, is a normalised eigenfunction of the Schrödinger equation for a particle of mass M and energy E in a one dimensional potential V(x) such that V(x) = 0 at x = 0. Find the value for V in units of 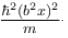
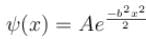 where A and B are real constant, is a normalised eigenfunction of the Schrödinger equation for a particle of mass M and energy E in a one dimensional potential V(x) such that V(x) = 0 at x = 0. Find the value for V in units of
where A and B are real constant, is a normalised eigenfunction of the Schrödinger equation for a particle of mass M and energy E in a one dimensional potential V(x) such that V(x) = 0 at x = 0. Find the value for V in units of 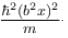
In the spectrum of hydrogen, what is the ratio of the longest wavelength in the Lymann series to the longest is Balmer series ?
In a photoelectric effect set up two metals with work function φ1 and φ2 are used. For the same value of incident frequency, the stopping potential for metal 1 is twice that for metal 2. If the incident energy is 5eV and the φ1 = 1.5eV. Find φ2. (in eV)
A particle is in an infinite square well potential with walls at x = 0 and x = L. If the particle is in the state  where A is a constant, what is the probability that the particle is between x = L/3 and x = 2L/3 upto 2 decimal places.
where A is a constant, what is the probability that the particle is between x = L/3 and x = 2L/3 upto 2 decimal places.
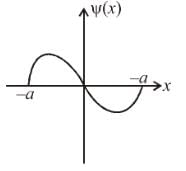
The figure shows one of the possible energy eigenfunction ψ(x) for a particle bouncing freely back and forth along the x-axis between impenetrable walls located at x ± a The potential energy equals zero for |x| < a. If the energy of the particle is 2eV when it is in the quantum state associated with its eigen function, what is its energy when it is in the quantum state of lowest energy (in eV)?
What is the probability of finding the particle in classically forbidden region in ground state of simple harmonic oscillator
An electron in a metal encounters a barrier layer of height 6eV and thickness 0.5 nm. If the electron energy of 5eV, what is the probability of tunneling through the barrier?
The energy of an electron moving in one dimension in an infinitely high potential box of width 1Å.
The solution of the schrödinger equation for the ground state of hydrogen is 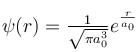 where a0 is the Bohr radius and r is the distance from the origin. The most probable value of r in units of a0.
where a0 is the Bohr radius and r is the distance from the origin. The most probable value of r in units of a0.
The density of a quantum system with two microstates is given by 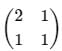 . Choose the correct option.
. Choose the correct option.


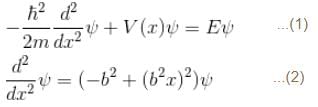
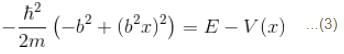
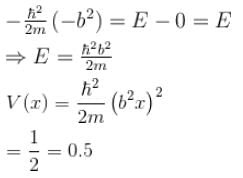
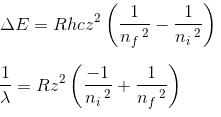


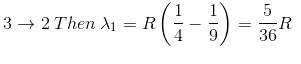
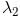 2 ---> 1
2 ---> 1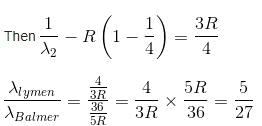

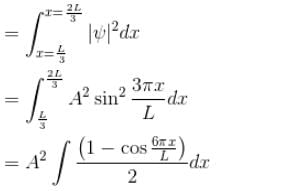
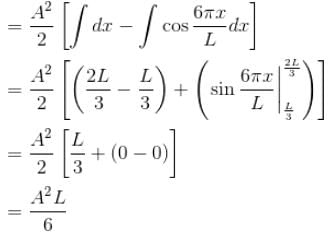
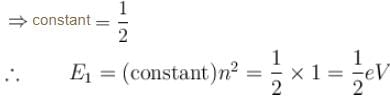
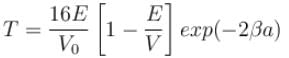
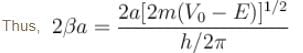
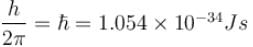
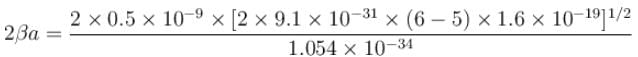
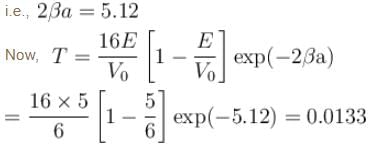
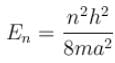
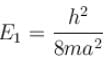 with h = 6.62 × 10–34 Js, m = 9.1 × 10–31 kg and a = 1 × 10–10 m
with h = 6.62 × 10–34 Js, m = 9.1 × 10–31 kg and a = 1 × 10–10 m