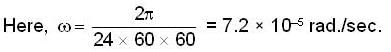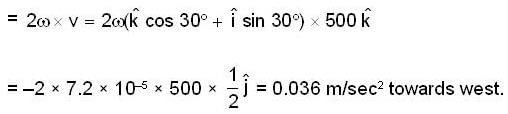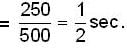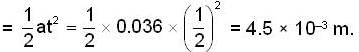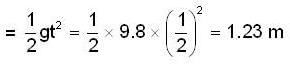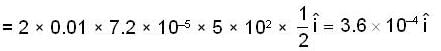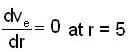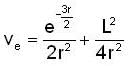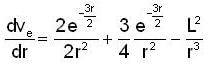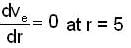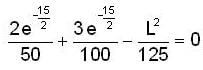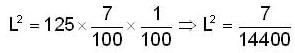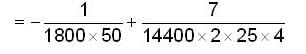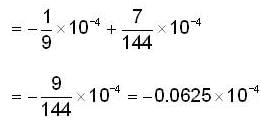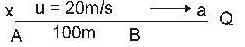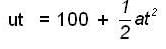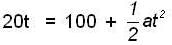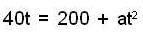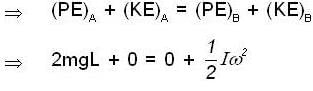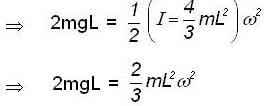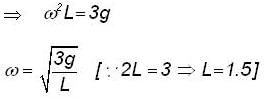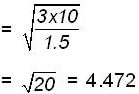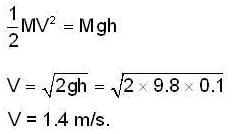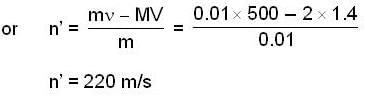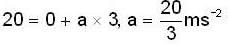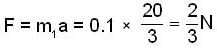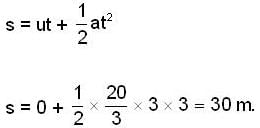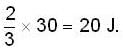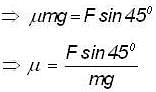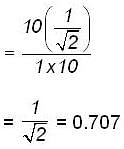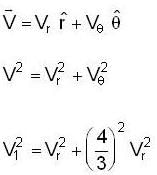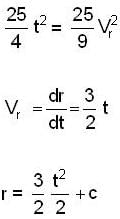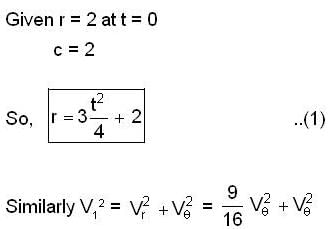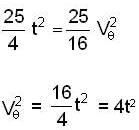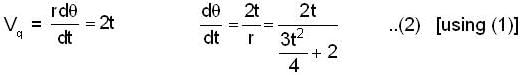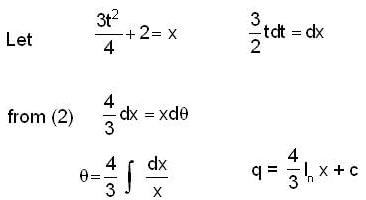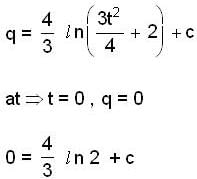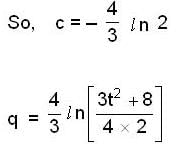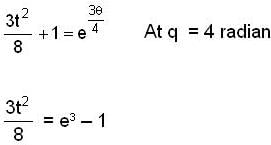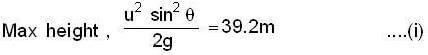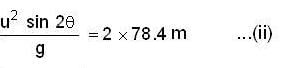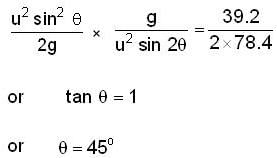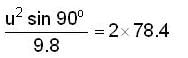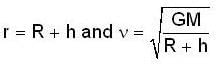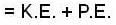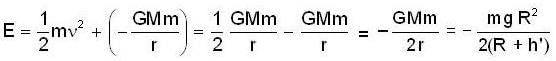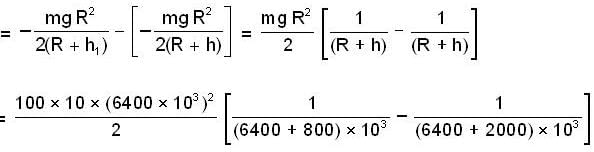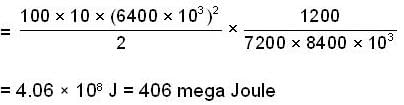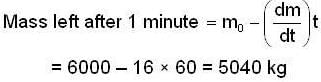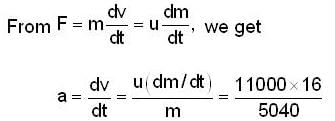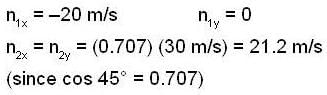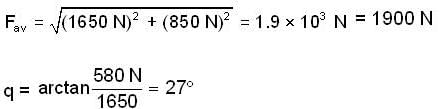IIT JAM Physics MCQ Test 1 - Physics MCQ
30 Questions MCQ Test IIT JAM Physics Mock Test Series 2025 - IIT JAM Physics MCQ Test 1
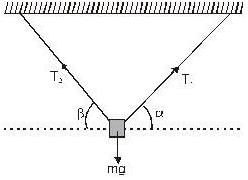
A body of mass m is suspended by two strings makings angle α and β with the horizontal. Find the tension T1 in the strings.
A body of mass 5 kg is acted upon by two perpendicular forces 8 N and 6 N. The magnitude and possible direction of the acceleration of the body are
The relation between time t and distance x is t = ax2 + bx where a and b` are constants. The acceleration is
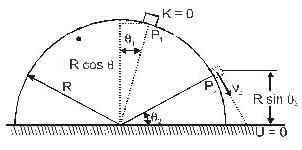
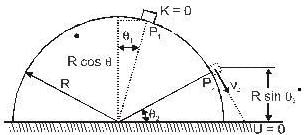
A particle moves from rest at P1 on the surface of a smooth circular cylinder of radius R as shown in Fig. At P2 the particle leaves the cylinder. The relation between θ1 and θ2 is:
The velocity of pendulum bob, which has been pulled aside from its equilibrium position through an angle θ and then released and it will pass through the equilibrium position, (where L is the length of the pendulum):
A rocket motor consumes one quintal of fuel per second. The exhaust speed of gasses w.r.t. rocket is 5 km/s. The force exerted on the rocket and velocity acquired by the rocket, when its mass reduces to 1/100th of its initial mass is:
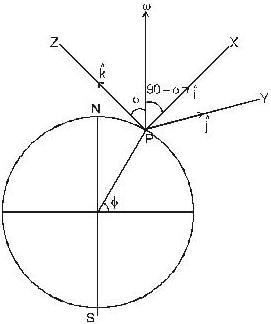
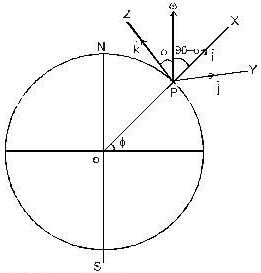
A bullet is fired horizontally in the north direction with a velocity of 500m/sec. at 300N latitude. The horizontal component of Coriolis acceleration is:
A canon launches a metal ball horizontal using a spring as the firing mechanism. The canon has mass mcanon and the mball. The spring constant is k. Initially, the spring is compressed a distance d from its equilibrium length. What is ncannon/nball, the ratio of the cannon's recoil velocity to the ball's velocity?
A satellite is in elliptical orbit about the earth (radius = 6400km). At perigee it has an altitude of 1100 km and at the apogee its altitude is 4100km.The major axis of the orbit is at the distance.
A particle describes a circular orbit under the influence of an attractive central force directed towards a point on the circle,then the force is inversely proportional to,
If f α -rn, then for what value of n, the circular orbit described is stable?
For a rigid body, linear velocity 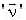 and angular velocity 'w' are related as;
and angular velocity 'w' are related as;
The linear mass density l of a rod, of uniform area of cross-section, 1 m long, varies with the distance x from its left end as given by
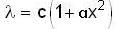
The centre of mass of the rod is located, from the left end, at a distance of:
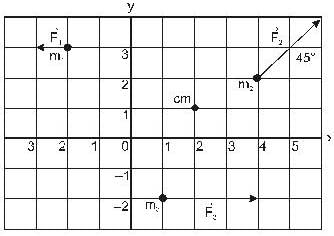
Figure shows a system of three initially resting particles of masses m1 = 4.1kg, m2 = 8.2kg./ and m3 = 4.1kg.The particles are each acted on by different net external forces, which have magnitudes F1 = 6N, F2 = 12N and F3 = 14N. The directions of the forces are shown in the figure. Where is the center of mass of this system?
Find the centre of mass of a uniform disc of radius a from whhich a circular section of radius b has been removed. The centre of hole is at a distance c from the centre of the disc.
A particle is moving in space with O as the origin. Some possible expressions for its position velocity and acceleration in cylindrical coordinate (p,φ,z) are given below, which of the following are correct?
For a particle moving in a central potential, which one of the following statements is correct?
A ball of mass m is thrown upward with velocity v and return back with v'. If air exerts an average resisting force F. Then
A bullet of mass 10gm is fired horizontally in the north direction with a velocity of 500m/sec at 300N latitude and it hits a target 250 meters away. Then
A body of mass 2 kg moves under the influence of a central force, with a potential energy function 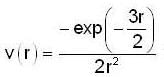 Joule, where r is the radius circular orbit and r = 5m
Joule, where r is the radius circular orbit and r = 5m 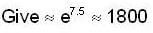
The corresponding angular momentum and total energy are L and E. Then
A man travelling in a car with a maximum constant speed of 20m/s watches his friend start off at a distance of 100m on a motor cycle with constant accelerationa. Then man in the car will reach his friend when a is .......m/sec2.
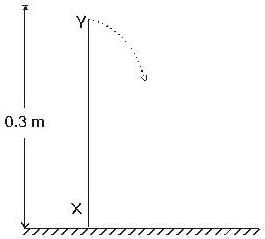
A thin uniform rod XY of mass 0.1 kg and length 0.3m is hinged at its lowe end at X to the horizontal floor. It originally stands vertical and is allowed to fall to the floor. It strikes the floor with an angular speed of (rad/sec).......
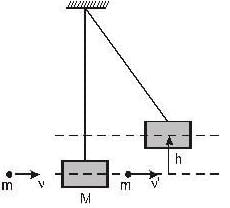
A bullet of mass 0.01kg and travelling at a speed of 500m/s strikes a block of mass 2 kg which is suspended by a string of length 5m. The centre of gravity of the block is found to rise a vertical distance of 0.1m. What is the speed(m/s) of the bullet after it emerges from the block? (g=9.8m/s2).
A toy rocket of mass 0.1 kg has a small fuel of mass 0.02kg which it burns out in 3s. Starting from rest on a horizontal smooth track, it gets a speed of 20 ms-1 after the fuel is burnt out. What is the approximate thrust of the rocket? What is the energy (joules/kg) content per unit mass of the fuel? (Ignore the small mass variation of the rocket during fuel burning)
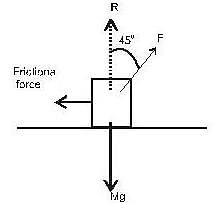
A wooden block having a mass of 1 kg is placed on a table. The block just starts to move, when a force of 10N is applied at 450 to the vertical to push the block. The coefficient of friction between the table and the block, (taking g = 10m/s2) is approximately________.
(Give answer upto two decimals)
A particle moves in a plane with velocity 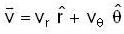 such that
such that 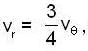 the time dependence of the magnitude of the velocity is
the time dependence of the magnitude of the velocity is  It is given that at
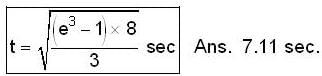
It is given that at 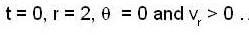 At what time (sec) will θ become 4 radian?
At what time (sec) will θ become 4 radian?
A boy stands at 78.4m from a building and throws a ball which just enters a window 39.2m above the ground Calculate the velocity of projection (ms-1) of the ball

A satellite of mass 100 kg is placed initially in a temporary orbit 800km above the surface of earth. The satellite is to be placed now in a permanent orbit at 2000km above the surface of earth. Find the amount of work done (mega joule) to move the satellite from temporary to permaanent orbit. The radius of the earth is 6400km. Given g = 10m/s2.
A rocket of initial 6000kg ejects mass at a constant rate of 16kg/s with constant relative speed of 11km/s. What is the acceleration (in m/s2) of the rocket on minute after blast?
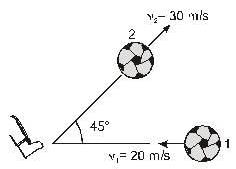
A soccer ball has a mass of 0.40kg. Initially, it is moving to the left at 20m/s but then it is kicked and given a velocity at 450 upward and to the right with a magnitude of 30m/s figure. Find the average net force (inN), asuming a collision time dt= 0.010s.
|
4 docs|21 tests
|


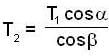 ....(3)
....(3)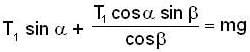

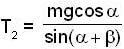
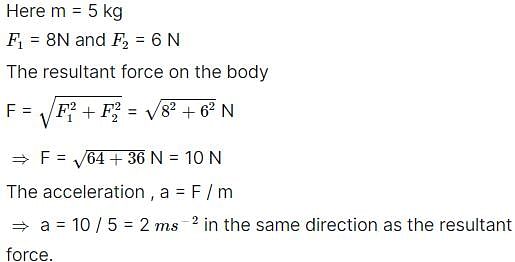
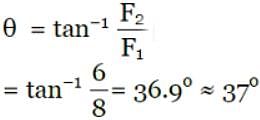

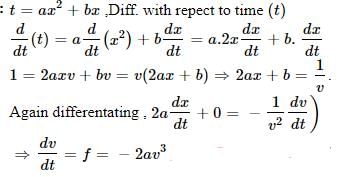
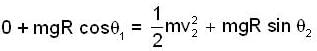
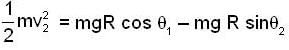
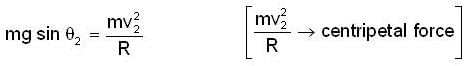
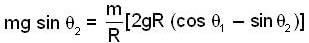 [using 2]
[using 2]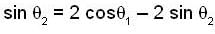
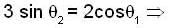
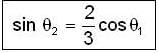
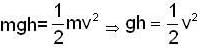
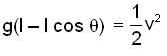
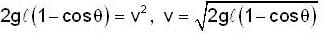
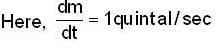
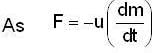

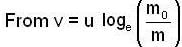
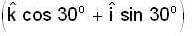 because the angular velocity vector w of the earth is directed parallel to its axis and is inclined at 300 to the horizontal
because the angular velocity vector w of the earth is directed parallel to its axis and is inclined at 300 to the horizontal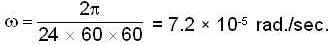
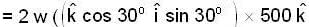
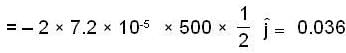 m/sec2 towards west.
m/sec2 towards west.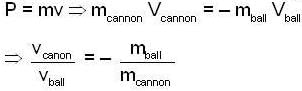
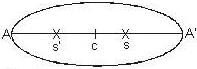
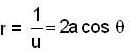
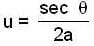 ...(1)
...(1) ...(2)
...(2)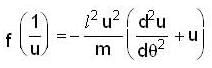
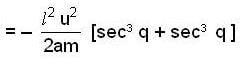
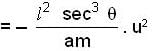
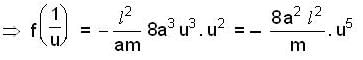

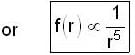
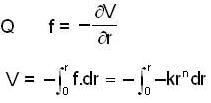
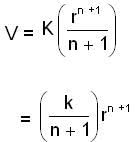
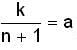 (new constant)
(new constant)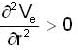
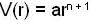 and centrifugal energy
and centrifugal energy 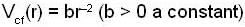
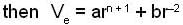
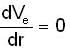
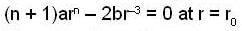
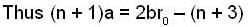 ...(2)
...(2)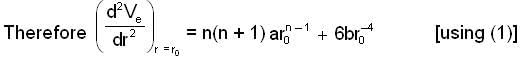
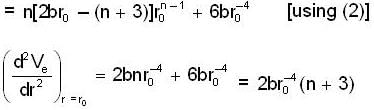
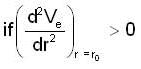

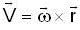
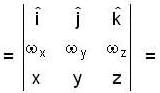
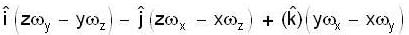
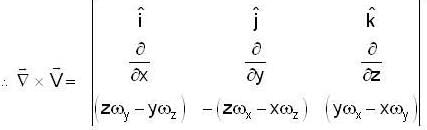
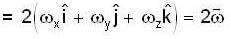
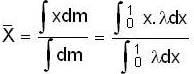 Q(dm = λdx)
Q(dm = λdx)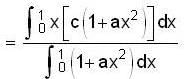

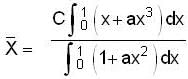
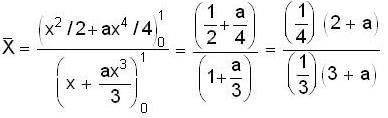
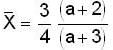
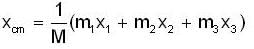

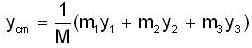

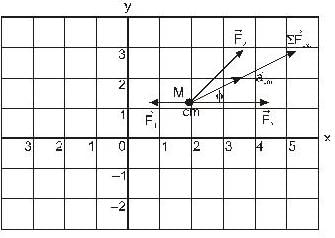
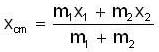 ...(i)
...(i)
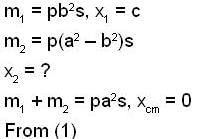
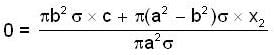
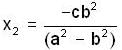


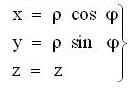
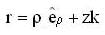
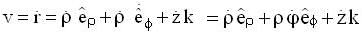
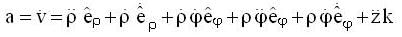
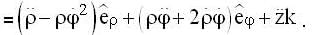
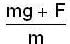
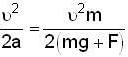
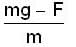
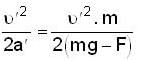
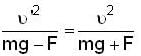
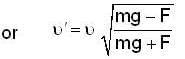
 because the angular velocity vector ww of the earth is directed parallel to its axis and is inclined at 300 to the horizibtal.
because the angular velocity vector ww of the earth is directed parallel to its axis and is inclined at 300 to the horizibtal.