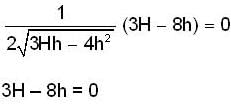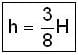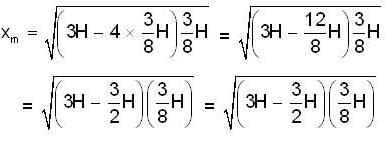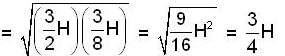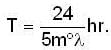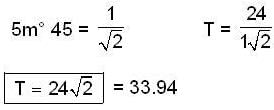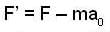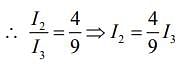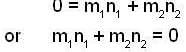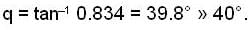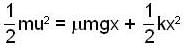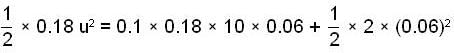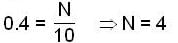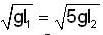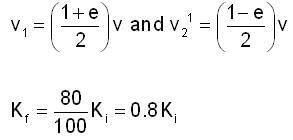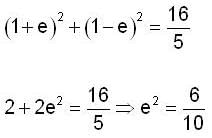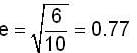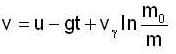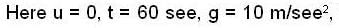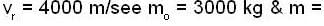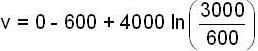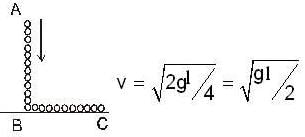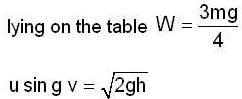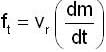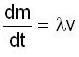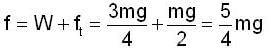IIT JAM Physics MCQ Test 2 - Physics MCQ
30 Questions MCQ Test IIT JAM Physics Mock Test Series 2025 - IIT JAM Physics MCQ Test 2
A bullet of mass m moving with a horizontal velocity n strikes a stationary block of mass M suspended by a spring of length L. The bullet gets embedded in the block. Prove that the maximum angle made the string after impact is
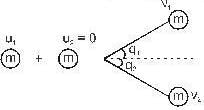
A sphere has a perfectly elastic oblique collision with another identical sphere which is initially at rest. The angle between their velocities after the collision is
A girl throws a ball with initial velocity u at an inclination of 45o. The ball strikes the smooth vertical wall at a horizontal distance d from girl and after rebounding returns to her hand. What is the coefficient of restitution between wall and ball?
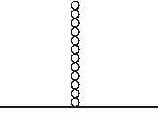
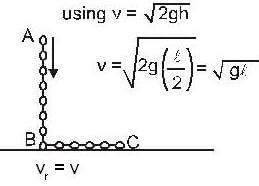
A uniform chain of mass m and length I hangs on a thread and touches the surface of a table by its lower end. Find the force exerted by the table on the chain when half of its length has fallen on the table. The fallen part does not form heap.

It l1 , l2 and l3 are the moments of inertia about, a diameter of a thin hollow sphere, solid sphere and disc having same mass and same radius respectively, then which one of the following is correct?
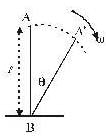
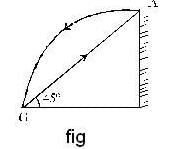
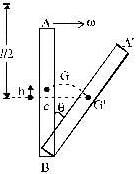
A uniform rod of length l is free to rotate in a vertical plane about a fixed horizontal axis through B. The rod begins rotating from rest from its unstable equilibrium position. When it has turned through an angle q, its angular velocity w is given as
Two bodies with moment of inertia l1 and l2 and (l1>l2) have equal angular momenta. If K.E. of rotation are E1 and E2 then
The object in Figure might be a billiard ball a steel ball bearing, or the world's largest ball of string. Find the moment of the inertia about an axis through the center of the sphere.
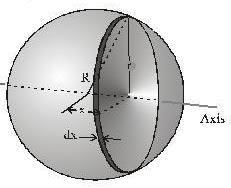
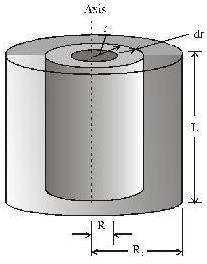
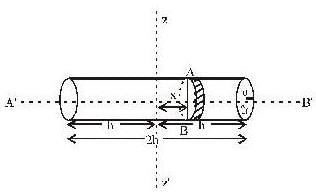
Figure shows a hollow, uniform cylinder with length L, inner radius R1, and outer radius R2, It might be a steel cylinder in a printing press or a sheet- steel rolling mill. The moment of inertia about the axis of symmetry of the cylinder is,
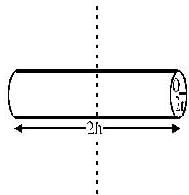
Moment of inertia of a solid cylinder of mass M height 2h and radius 2r about an axis (shown in the figure by dahsed line) passing through its centre of mass and perpendicular to its symmetry axis is
Consider the following statements with reference to X-rays:
1. They produce heat when absorbed by matter.
2. They are generated when fast-moving electrons strike a metal target.
3. They can penetrate through a thin sheet of aluminium.
Which of the statements given above are correct?
Two particles A and B initially at rest, moves towards each other under a mutual force of attraction. If at an instant the speed of A is V and that of B is 2V then the speed of the centre of mass of the system is
Radioactive 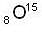 decays into
decays into 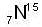 by emitting a positron and a neutrino. The positron and the neutrino are observed t move at right angles to each other and carry momenta 2 x 10-22 and 5 x 10-23 kg msec-1 respectively. Then the momentum of the recoiling nucleus is
by emitting a positron and a neutrino. The positron and the neutrino are observed t move at right angles to each other and carry momenta 2 x 10-22 and 5 x 10-23 kg msec-1 respectively. Then the momentum of the recoiling nucleus is
A uniform chain of mass m and length I hangs on a thread and touches the surface of a table by its lower end. find the force exerted by the table on the chain when half of its length has fallen on the gable. The fallen part does not from heap.
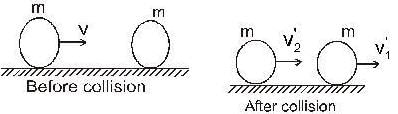
Two objects of masses m1 = 200 gm and m2 = 500gm possess velocities  just prior to a collision during which they become permanently attached to each other.
just prior to a collision during which they become permanently attached to each other.
A particle is released at x = 1 in a force field  which one of the following statement is true?
which one of the following statement is true?
A particle is acted upon by a force 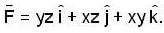 Which of the following statements are false?
Which of the following statements are false?
The stream function 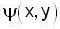 of two dimensional flow field is given by
of two dimensional flow field is given by 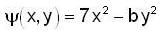
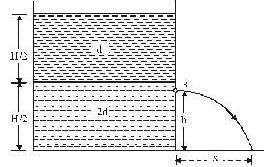
A container of large uniform cross-sectional area A resting on a horizontal surface has two immiscible, non-viscous and incompressible liquids of densities d and 2d, each of height H/2 as shown. The lower density liquid is open to the atmosphere having pressure P0. A tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h (h < H/2). Determine:
At what time a Foucault's pendulum completes a round when it is at 450N latitude on north pole?
An astronaut travelling in a rocket moving vertically upwards with an acceleration of 4g weighs 300kg. Then find out the weight (in Kg) of the astronaut in the laboratory.
The intensity of the primary maximum in a two-slit interference pattern is given by I2 and the intensity of the primary maximum in a three-slit interference pattern is given by I3. Assuming the far-field approximation, the same slit parameters and intensity of the incident light in both the cases, I2 and 3 I3 are related as
A bullet of mass 10 g. is fired with a speed of 1,000 m/s. from a freely hanging gun of mass 2 kg. Calculate the recoil velocity of gun (in m/s).
Two skaters collide and embrace, in a completely in elastic collision. That is they stick together after impact, as suggested by figure, where the origin is placed at the point of collision. Alfred, whose mass mA is 83 kg, is originally moving east with speed nA = 6.2 km/h. Barbara, whose mass mB is 55 kg is originally moving north with speed nB = 7.8 km/h.
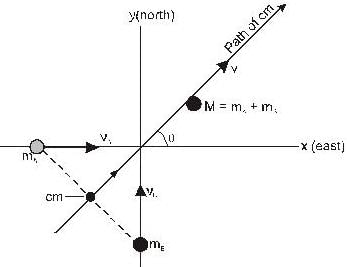
What is the velocity (km/hr) v of the couple after impact?
A block of mass 0.18 kg is attached to a spring of force constant 2 N/m. The coefficient of friction between the block and the floor is 0.1. Initially, the block is at rest and the spring is un-stretched. An impulse is given to the block as shown in the figure. The bock slides a distance of 0.06m and comes to rest for the first time. The initial velocity of the block in m/sec is V = N/10. Then N is....
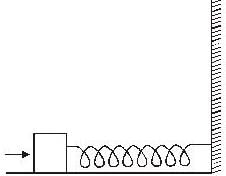
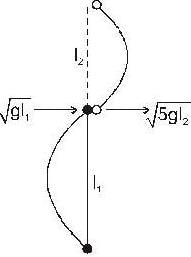
A bob of mass m, suspended by a string of length l1, is give a minimum velocity required to complete a full circle in the verticle plane. At the highest point, it collides elastically with another bob of mass m suspended by a string of length l2, which is initially at rest. Both the strings are mass-less and inextensible. If the second bob, after collision acquires the minimum speed required to complete a full circle in verticle plane, the ration l1/l2 is ...
A ball of mass m moving at a speed v makes a head-on wllision with an identical ball at rest. The kinetic energy of the balls after the collision is 80% of the original. Find the coefficient of restilation.
A rocket, with an initial mass of 3000kg, is launched vertically upwards from rest under gravity. The rocket burns fuel at the rate of 40 kg per deeond. The burnt watter is ejected vertically downwards with a speed of 4000 m/see relative to the rocket. If burning stops after one minute. Find the maximum velocity of rocket.
A uniforem chain of mass m and length I hangs on a thread and touches the surface of a lable by its lower end. Find the force exerted by the table on the chain when three-founth of its length has ballen m the lable. The fallen part does not form heap.
|
4 docs|21 tests
|



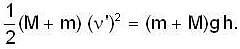 .....(2)
.....(2)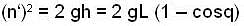 ....(4)
....(4)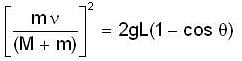


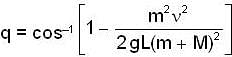
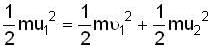 ....(3)
....(3)


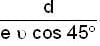
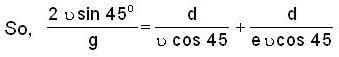
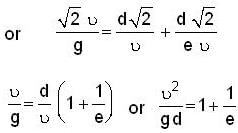
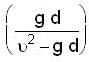
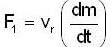

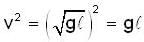
 (downwards)
(downwards)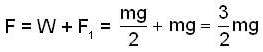


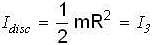

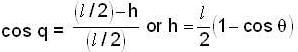
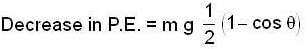 ..(1)
..(1)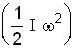
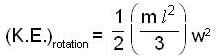 ...(2)
...(2)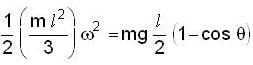

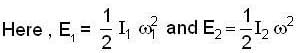
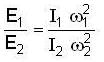 ...(i)
...(i)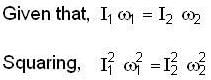
 ...(ii)
...(ii)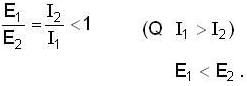
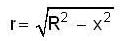

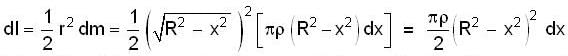

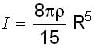
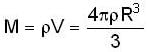
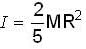
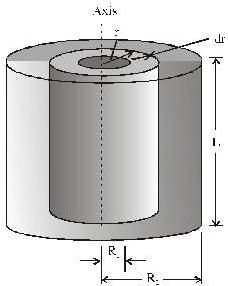
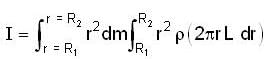 [use equation(1)]
[use equation(1)]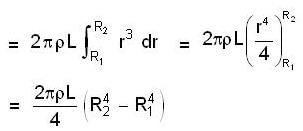
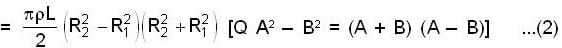
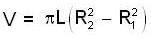 [Volume of the cylinder V = pR2h] ...(4)
[Volume of the cylinder V = pR2h] ...(4)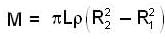 ...(5)
...(5)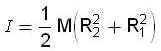
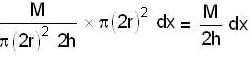
 is mass per unit volume
is mass per unit volume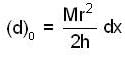
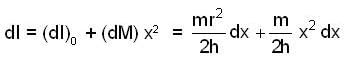
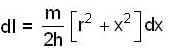






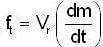
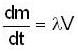
 is mass per unit length of chain
is mass per unit length of chain 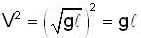
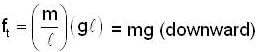
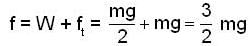
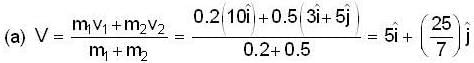
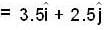
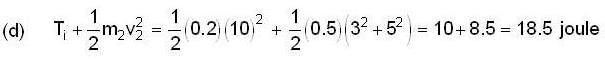
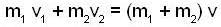
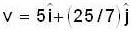
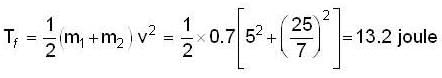
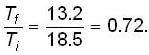

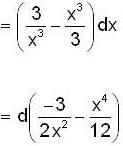
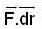 is exact differential work done by this force is independent of path. So the force is conservative
is exact differential work done by this force is independent of path. So the force is conservative
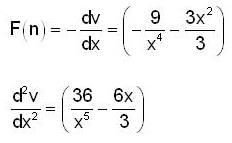

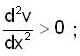 so potential energy is minimum at x = 3 1/3
so potential energy is minimum at x = 3 1/3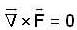
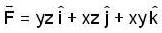
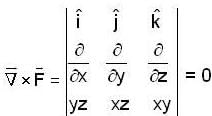
 is conservative then a scalar potential v exist such that
is conservative then a scalar potential v exist such that 


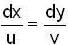

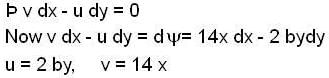
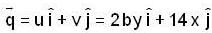
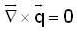
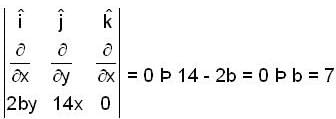

 the velocity of fluid
the velocity of fluid 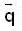 can be expressed as gradient of scaler potential
can be expressed as gradient of scaler potential 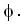
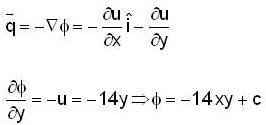
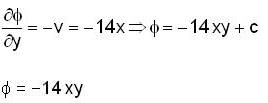
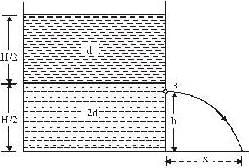

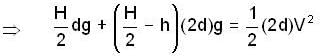

 ...(i)
...(i)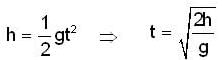 ....(ii)
....(ii)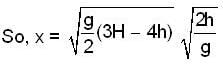 [use equation (1) and (2)]
[use equation (1) and (2)]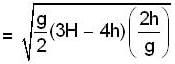
 ...(iii)
...(iii)