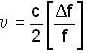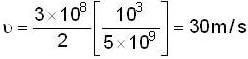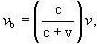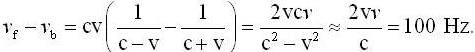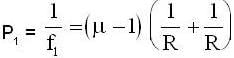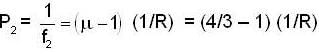IIT JAM Physics MCQ Test 3 - Physics MCQ
30 Questions MCQ Test IIT JAM Physics Mock Test Series 2025 - IIT JAM Physics MCQ Test 3
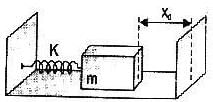
One end of a spring having force constant K is fixed to a vertical wall and other to a body of mass m resting on a smooth horizontal surface. There is another wall at a distance x0 from the body. The spring is then compressed by 2x0 and released. The time taken to strike the wall from its compressed position is

A particle executing S.H.M. in a straight line has velocities 8, 7, 4 at three points distant one foot from each other. The maximum velocity of the particle will be
A particle is vibrating in simple harmonic motion with an amplitude of 4 cm. At what displacement from the equilibrium position is its energy half potential and half kinetic?
A particle of mass m is attached to three springs A, b and C of equal force constants k. Fig.
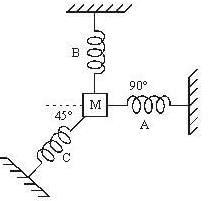
The particle is pushed slightly against the spring C and released the time period of oscillation will be
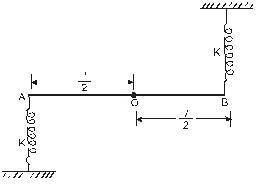
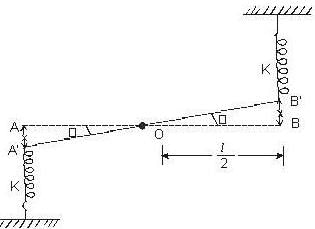
The ends of a rod of length / and mass m are attached to two identical springs as shown in figure. The rod is free to rotate about its centre O. The rod is depressed slightly at end A and released. The time period of the resulting oscillation is
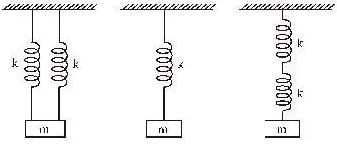
In the case of suspensions shown in the given diagrams, the natural frequencies of the three simple harmonic oscillators will be in the ratio of :
When a harmonic waves is propagating through a medium, the displacement y of a particle of the medium is represented by y = 10 sin 2π/5 (1800 t-x)
The time period will be:
Two particles execute simple harmonic motions of the same amplitude and frequency along the same straight line. They pass one another travelling in opposite directions, whenever their displacement is half of their amplitude. The phase difference between the two is :
A particle is acted upon by two simple harmonic motions,
x = a sin (ωt + φ)
and y = b sin ωt
Which one of the following diagrams correctly gives the resultant path of the particle when 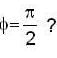
Among the following displacement versus time plots, which ones may represent an overdamped oscillator?
At the instant t = 0, a particle starts moving due to a force F = F0 sinωt, where F0, ω are constants. Which one of the following plots gives the relation between the distance(s) covered by the particle and ωt
A mass M is suspended from a light spring. An additional mass m added displaces the spring further by a distance x. Now the combined mass will oscillate on the spring with a period :
Among the following displacement versus time plots, which ones may represent a damped oscillator?
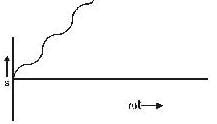
The instantaneous position x(t) of a small block performing one-dimensional damped oscillation is x(t) =  Here, ω id the angular frequency γ the damping coefficient, A the initial amplitude and α the initial phase. If
Here, ω id the angular frequency γ the damping coefficient, A the initial amplitude and α the initial phase. If 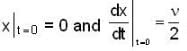 the value of A and α (with n = 0, 1, 2...) are
the value of A and α (with n = 0, 1, 2...) are
A man stands on a weighing machine placed on a horizontal platform. The machine reads 50kg. By means of a suitable mechanism the platform is made to execute harmonic vibrations up and down with a frequency of 2 vibrations per second. What will be the effect on the reading of the weighing machine? The amplitude of vibration of the platform is 5 cm. Take g = 10ms-2
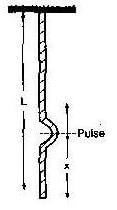
If a tunnel is dug through the earth from one side to the other side along a diameter. Show that the motion of a particle dropped into the tunnel is simple harmonic motion. Find the time period. Neglect all the frictional forces and assume that the earth has a uniform density.
G = 6.67 x 10-11 Nm2 kg-2; density of earth = 5.51 x 103 kg m-3
A particle-free to move along the X-axis has potential energy given by U(x) = k [1-exp(-x2)] for 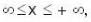 where k is a positive constant of appropriate dimensions. Then which of the following are incorrect?
where k is a positive constant of appropriate dimensions. Then which of the following are incorrect?
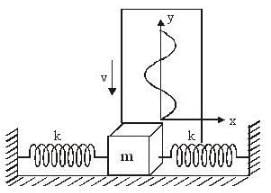
One end of each of two identical springs, each of force constant 0.5 N/m, are attached on the opposite sides of a wooden block of mass 0.01 kg. The other ends of the springs are connected to separate rigid supports such that the springs are unstretched and are collinear in a horizontal plane. To the wooden piece kept on a smooth horizontal table is now displaced by 0.02m along the line of springs and released. If the speed of the paper is 0.1 m/s, then which of the following are correct ?
Which of the following statements are correct when white light is incident on a zone plate from a point?
When an unpolarised light beam passes through a double refracting medium, it splits up into two beams called ordinary ray and extraordinary ray. Which of the following statements are correct?
A horizontal platform executes up and clown S.H.M. about a mean position. Its period is 2π sec. A mass m is resting on the platform. The greatest value of amplitude (in m) so that the mass ‘m' may not leave the platform i s _________ .
A uniform rope of mass 0.1 kg and length 2.45 m hangs from a ceiling. Find the speed (in m/s) of transverse wave in the rope at a point 0.5m distant from the lower end, (g = 9.8 m/s2)
A uniform rope of mass 0.1 kg and length 2.45 m hangs from a ceiling. Calculate the time (in sec) taken by a transverse wave to travel the full length of the rope (g = 9.8 m/s2)
A source of sound S is moving with a velocity 50 m/s towards a stationary observer. The observer measures the frequency of the source as 1000 Hz. What will be the apparent frequency (in Hz) of the source when it is moving away from observer after crossing him ? The velocity of sound in the medium is 350 m/s.
The mass and diameter of a planet are twice those of the earth. The time period (in sec) of a simple pendulum on this planet is _________ , if it is second's pendulum on earth .
The vibration of a string can be described by the equation y = (0.75 cm) {cos(2π/ 5cm-1)x} sin{(60πs-1)t}. The speed (cm/s) of the waves travelling in the string is_______
An astronaut is approaching the moon. He sends out a radio signal of frequency 5 * 109 Hz and finds out that the frequency shift in echo received is 103 Hz. Find his speed (in m/s) of approach.
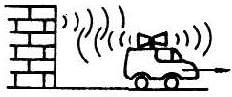
A car has front - and back - directed speakers mounted on its roof, and drives toward you with a speed of 50 ft/s, as shown in figure. If the speakers are driven by a 1000 Hz oscillator, what beat frequency (in Hz) will you hear between the direct sound and the echo off a brick building behind the car ? (Take the speed of sound as 1000 ft/s.).
The focal length of a piano convex lens, the convex surface of which is silvered, is 0.3 m. If μ of the lens is (7/4), the radius of curvature (in m) of convex surface is____
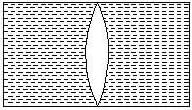
A thin-walled cell of transparent material contains a glass convex lens of μ = 1.5 and radii of curvature 10 cms each exactly at its middle. The empty spaces are filled with a liquid of μ = 4/3. Calculate the power (in diopter) o f the system.
|
4 docs|21 tests
|


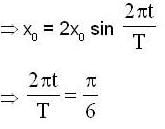
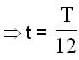
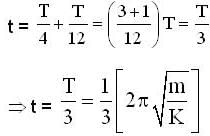
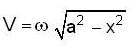
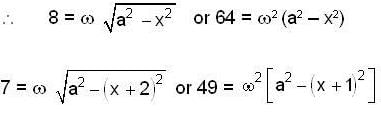
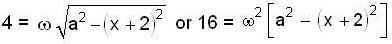
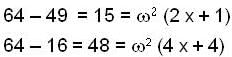
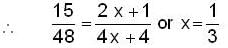
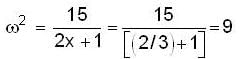
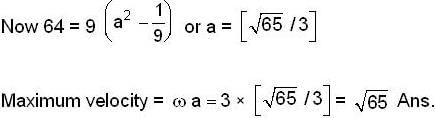

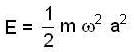 ...(1)
...(1)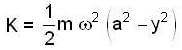
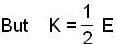
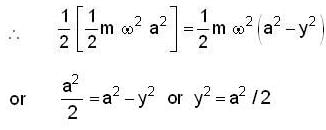
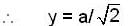
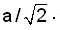 Given that a = 4cm.
Given that a = 4cm.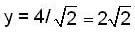


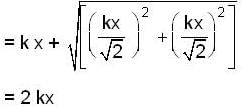
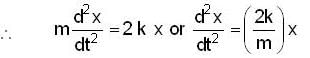

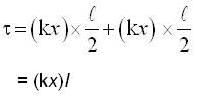
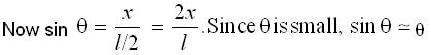
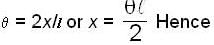
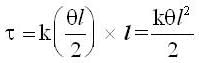
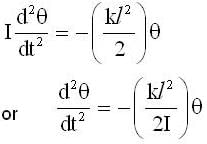
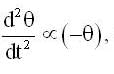 the motion is simple harmonic whose angular frequency is given by
the motion is simple harmonic whose angular frequency is given by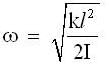
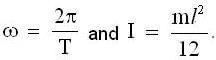 Therefore we have
Therefore we have 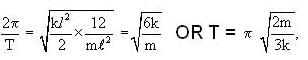

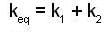
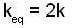 (since K1 = K2)
(since K1 = K2)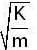
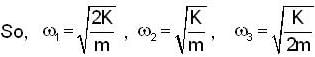
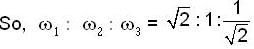
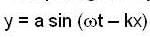
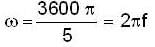 ...(1)
...(1)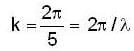 ..(2)
..(2)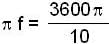
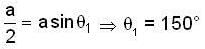
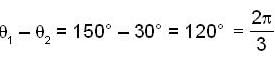
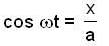
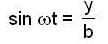
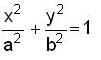
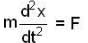
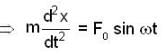
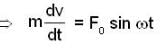
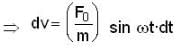
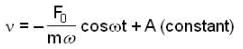
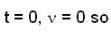
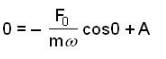
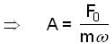
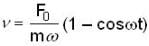
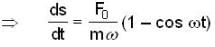
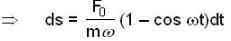
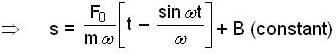
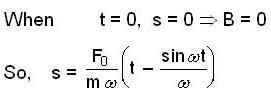


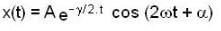
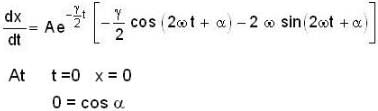
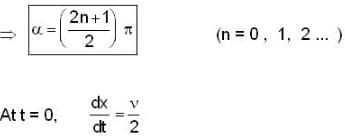
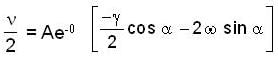
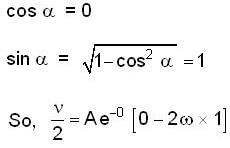
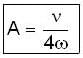
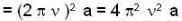
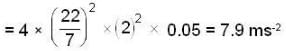
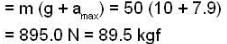
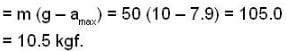

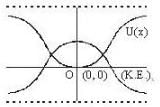
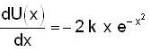
 ) the particle is not even in equilibrium.
) the particle is not even in equilibrium.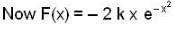
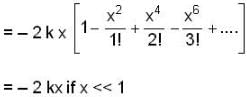
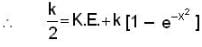
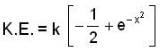
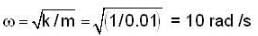
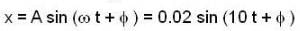 ..(i)
..(i)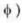
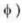 = max = 1,
= max = 1, 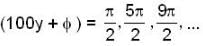

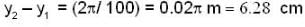
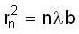
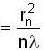

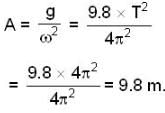
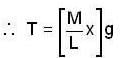
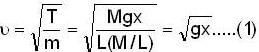
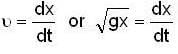 [from eq. 1]
[from eq. 1]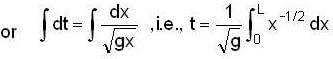
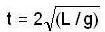 [from eq. 2]
[from eq. 2]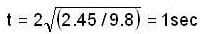

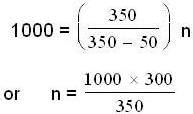
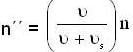
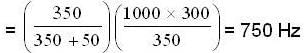
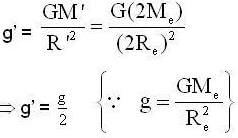
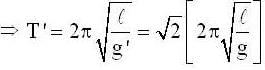

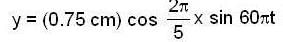 Comparing this with the standard equation of standing wave given as
Comparing this with the standard equation of standing wave given as
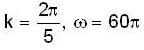
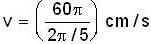 = 150 cm/s
= 150 cm/s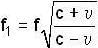 ...(1)
...(1)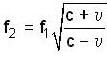 ...(2)
...(2)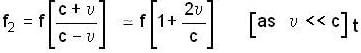
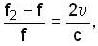 i.e
i.e