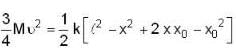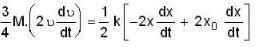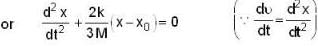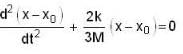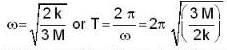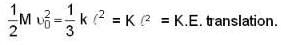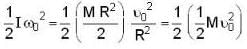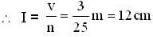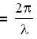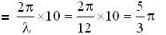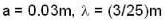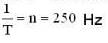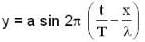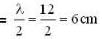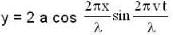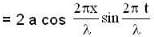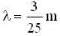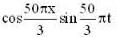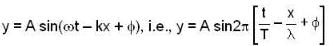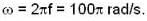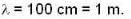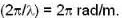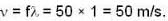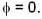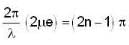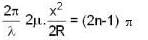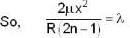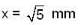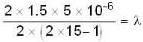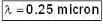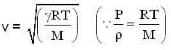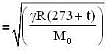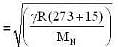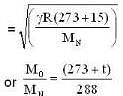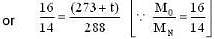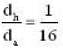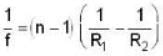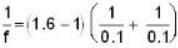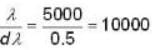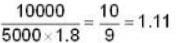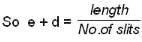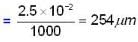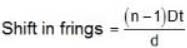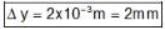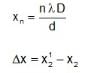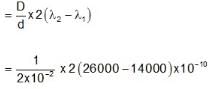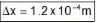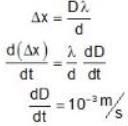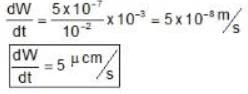IIT JAM Physics MCQ Test 4 - Physics MCQ
30 Questions MCQ Test IIT JAM Physics Mock Test Series 2025 - IIT JAM Physics MCQ Test 4
What are the values of phase velocity and group velocity respectively of the de- Broglie wave describing a free electron with velocity?
If the dispersion relation for electromagnetic waves of wave vector k in the ionoshpere is 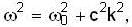 , then the group velocity vg and phase velocity vp are related as :
, then the group velocity vg and phase velocity vp are related as :
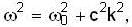 , then the group velocity vg and phase velocity vp are related as :
, then the group velocity vg and phase velocity vp are related as :| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If waves in an ocean travel with a phase velocity 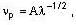 then what is the group velocity vg of the ‘wave packet' of these waves?
then what is the group velocity vg of the ‘wave packet' of these waves?
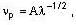 then what is the group velocity vg of the ‘wave packet' of these waves?
then what is the group velocity vg of the ‘wave packet' of these waves?The relation between angular frequency 00 and wave number K for given type of waves is 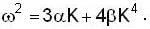 . The wave number K0 for which the phase velocity equal the group velocity is
. The wave number K0 for which the phase velocity equal the group velocity is
A travelling wave is represented by— 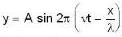 If die ratio of the wave velocity to the peak particle velocity is 10. then the amplitude A is equal to :
If die ratio of the wave velocity to the peak particle velocity is 10. then the amplitude A is equal to :
The relation between wavelength and frequency for a waveguide is given s 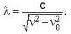 calculate the group velocity of the wave .
calculate the group velocity of the wave .
A person hears the sound of jet aeroplane after it has passed over his head. The angle of the jet plane with the horizontal when the sound appears to be coming vertically downwards is 60°. If the velocity of sound is v, then the velocity of the jet plane should be
A sound source with frequency f0 moves with a speed u towards a stationary wall. The speed of sound is v. The frequency detected by an observer moving together with source with same speed u is
A source of sound approaches an observer and then recedes from it. Ratio of frequencies of sound as the source approaches and as the source recedes is 6 : 5. Find the velocity of source (Velocity of sound = 330 ms-1)
A fire alarm sounds with a frequency of 480 Hz. Two fire engines dash to the site to extinguish the fire from opposite directions. One travels with a speed of 33 m/s and the other with 27m/s. If the velocity of sound in air be 330 m/s, the difference between the frequencies of the sirens are heard by the drivers of the two fire engines will be :
A particle is executing simple harmonic motion. What is the nature of the graph of velocity as a function of displacement?
Consider the following statements about a harmonic oscillator: -
1. The minimum energy of the oscillator is zero.
2. The probability of finding it is maximum at the mean position.
Which of the statement given above is/are correct ?
What is the phase difference between the two simple harmonic vibrations represent by .

A particle is executing SHM. If the displacement at any instant is given by x = 3 c o s 2 + 4 s in 2 t. What is the time period of the particle?
An object of small size and mass m is attached to a spring of force constant K fixed at one end and is undergoing linear oscillatory motion. If its maximum displacement from the point of equilibrium is x. What is its speed, when it is at A = x0
Consider two waves represented by two mutually perpendicular electric field vectors :  Their superposition will result in a plane polarized light, if:
Their superposition will result in a plane polarized light, if:
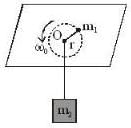
In the arrangement shown in figure, the particle m1 rotates in a radius r on a smooth horizontal surface with angular velocity ω0. Then choose the correct statement.
A solid cylinder of mass M is attached to horizontal spring of force constant k as shown in figure. The spring is first stretched by.
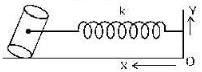
length l, by moving cylinder to the left. When the system is released from rest, the cylinder rolls along the horizontal surface without slipping. Centre of mass of the cylinder executes simple harmonic motion.
A progressive and a stationary simple harmonic wave each has the same frequency of 250Hz, and the same velocity of 30 m/s. Then which of the following are correct.
The equation for the displacement of a stretched string is given by y = 4 sin 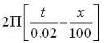 where y and x are in cm and t is in sec . Which of the following are correct.
where y and x are in cm and t is in sec . Which of the following are correct.
The spherical surface of a plane -convex lens of radius of curvature R = 2m is gently placed on a flat plate. The space between them is filled with a transparent liquid of refractive index 1.5. The refractive indices of the lens and the flat are 1.4 and 1.6 respectively. The radius of the fifteen dark newton's ring in the reflected light of wavelength λ is found to be √5m.m. Determine the wave length λ (in microns) of the light.
The ratio in the densities of oxygen and nitrogen is 16 : 14. At what temperature (in °C) the speed of sound will be the same which is in nitrogen at 15°C.
The speed of sound at NTP in air is 332 m/sec. Calculate the speed (in m/sec) of sound in hydrogen at NTP (Air is 16 times heavier than hydrogen.)
The speed of sound at NTP in air is 332 m/sec. Calculate the speed (in m/ s) of sound in hydrogen at 8190C temperature and 4 atmospheric pressure (Air is 16 times heavier than hydrogen.)
The power (in diopters) of an equiconvex lens with radii of curvature of 10 cm and refractive index o f 1.6 i s ________ .
A parallel beam of light of diameter 1.8cm contains two wavelengths 4999.75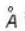 and 5000.25
and 5000.25 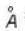 . The light is incident perpendicularly on a large diffraction grating with 5000 lines per centimeter using Rayleigh criterion the least order at which the two wave / lengths are resolved i s _______ .
. The light is incident perpendicularly on a large diffraction grating with 5000 lines per centimeter using Rayleigh criterion the least order at which the two wave / lengths are resolved i s _______ .
A diffraction grating of length 2.5 - 1 0-2 m is illuminated by a light with two wavelengths 5997 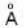 and 6003
and 6003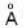 . The maximum size of the grating element d ( in μm ) required to resolve the two wavelengths in the first order is ______ .
. The maximum size of the grating element d ( in μm ) required to resolve the two wavelengths in the first order is ______ .
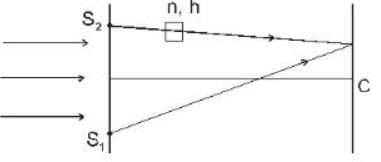
A plane monochromatic light wave falls normally on a diaphrapm with two narrow slits separated by a distance d = 2.5 mm. A fringe pattern is formed on a screen placed at a distance I = 100cm behind the diaphrapm. By what distance and in which direction will these fringes be displaced when one of the slits is covered by a glass plate of thickness h = 10μm (in mm).
A parallel beam of EM waves consistings of two wavelength 14000  and 26000
and 26000  coherent in themselves falls on a double slit apparatus. The separation between the two slits is 2 cm and that between plane of the slits at screen is 1 metre.
coherent in themselves falls on a double slit apparatus. The separation between the two slits is 2 cm and that between plane of the slits at screen is 1 metre.
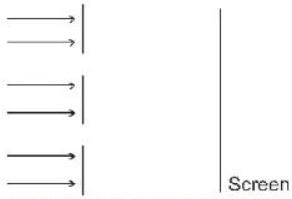
Find out the separation between the 2nd maxima formed by each wavelengths, (in 10-4 m)
The figure shows a YDSE arrangment. Given :d = 1 cm. D = 100cm, λ = 5000 . If the screen is given an instantaneous velocity of 1 mm per second towards right from the slits.
. If the screen is given an instantaneous velocity of 1 mm per second towards right from the slits.
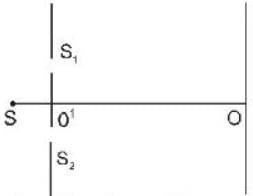
Then what is the rate of change of fringe width?
in (μ cm/sec).
|
4 docs|21 tests
|


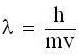
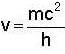

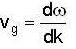
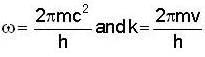
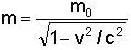
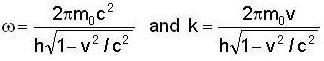
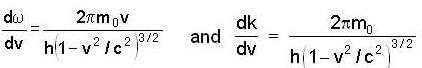
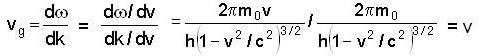
 ...(i)
...(i)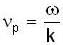 ...(ii)
...(ii)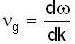 ...(iii)
...(iii)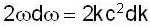
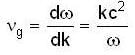 ...(iv)
...(iv)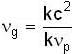 ⇒
⇒ 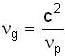 ⇒
⇒ 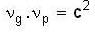
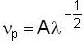

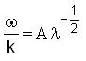
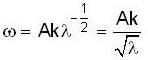
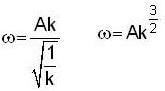 ...(iii)
...(iii)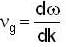
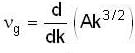
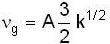
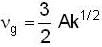
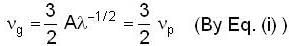
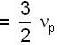
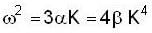
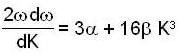
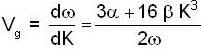
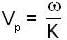
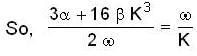
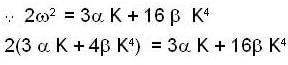
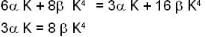

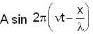

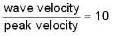
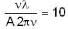
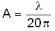
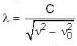
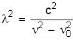 or
or 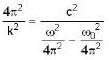


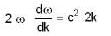
 Ans.
Ans.
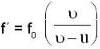
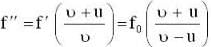
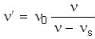
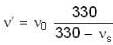 ...(i)
...(i)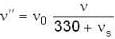
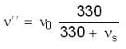 ...(ii)
...(ii)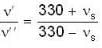
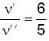
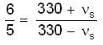
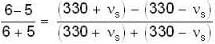


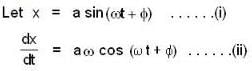



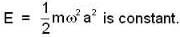


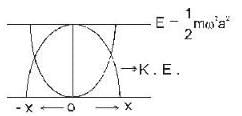
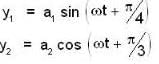
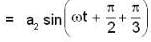
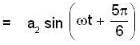
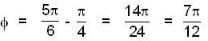

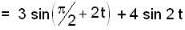

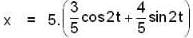
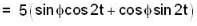
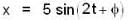
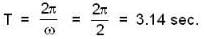
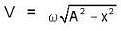
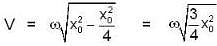
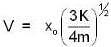

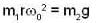
 ...(i)
...(i)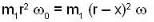
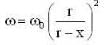 ...(ii)
...(ii)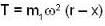
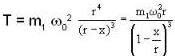
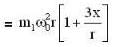 ...(iii)
...(iii)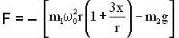
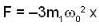 ...(iv)
...(iv)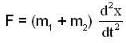 ...(v)
...(v)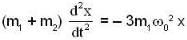
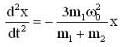 ...(vi)
...(vi)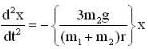
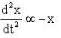
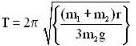
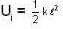
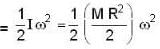
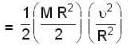

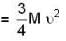 ...(i)
...(i)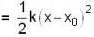
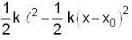
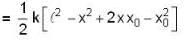 ...(ii)
...(ii)