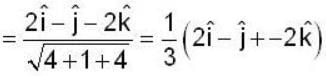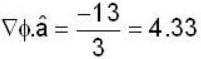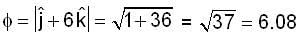IIT JAM Physics MCQ Test 8 - Physics MCQ
30 Questions MCQ Test IIT JAM Physics Mock Test Series 2025 - IIT JAM Physics MCQ Test 8
The latent heat of water diminishes by 0.695 cal./gm. for each degree centigrade rise in temperature at temperature 1000 and latent of water vapour at 100°C, is 540 cal.gm. The specific heat for saturated steam is
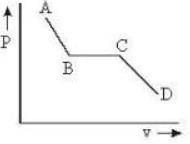
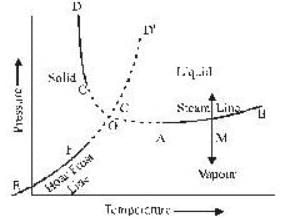
The portion AB of the indicator diagram representing the state of matter denotes

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Mercury melts at-38.87°C at 1 atmosphere pressure and it's density is 13.59 g/ c.c. The density of the solid is 14.19 g/c.c. The heat of fusion is 2.33 cal/g. What would be the melting point of mercury at 1000 atmosphere?
Calculate the latent heat of ice given that change of pressure by one atmosphere changes the melting point of ice by 0.0074oC and when one gm. of ice melts its volume changes by 0.0907 c.c.
A system of non-interacting fermi particles with fermi energy εf has the density of states proportional to √ε where ε is the energy of the particle. Then the average energy per particle at temperature T = 0 K is
The coordinates of the triple point of water are t = 0.0075oC and p = 0.0060 atmosphere. Calculate the slope of the ice line in atoms /oC.
Fermi function 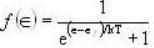 gives the probability of occupation of electrons per energy state. Then the probability of number of electrons at absolute temperature (T = 0 K) when ε=εf is
gives the probability of occupation of electrons per energy state. Then the probability of number of electrons at absolute temperature (T = 0 K) when ε=εf is
Fermi energy of conduction electron in silver is 5.48 eV. Then the number of such electrons per cm3 given that h = 6.62 x 10-2 erg-sec. and 1 eV = 1.6 * 10-12 erg will be
A mass m of water at temperature T1 K is isobarically and adiabatically mixed with an equal mass of water at T2 K. The entropy change of the inverse is
1 g of perfect gas at volume v A, pressure pA and temperature TA changes from state A to state B when volume is V0, pressure is pB and temperature TB. The change in entropy is
A body P(temperature Tp) has twice the mass and twice the specific heat compared to that of the body Q (temperature TQ). If the bodies are supplied equal amount of heat, the relationship between their resulting temperature changes (Δ Tp and Δ TQ) will be
A flask containing 1 mole of oxygen gas is known to contain a mixture of O and O2 molecules. The specific heat of the gas is found to be 17/10 R, where R is the gas constant. The number n1 of O1 atoms and the number n2 of O2 molecules are in the ratio (n1: n2)
A heating element weighing 100 g made of a material with specific heat of 1J/ (gC) is exposed to ambient air at 30°C and attains a steady-state temperature of 130°C while absorbing 100 W of electric power. Neglecting radiation, the time taken for the heating element to cool to 129° C after the power is switched off is most nearly equal to
A block made of a metal with specific heat C resting on a horizontal wooden board is imparted a speed v by an impulse. The metal block comes to rest due to friction with the wooden board (coefficient of kinetic friction μ). If all the heat generated by the friction is absorbed by the metal block, its temperature rises by
Two vessels separately contain two ideal gases A and B at the same temperature, the pressure of A being twice that of B. Under these conditions, the density of A is found to be one and halftimes the density of B. The ratio of molecular weights of A and B is
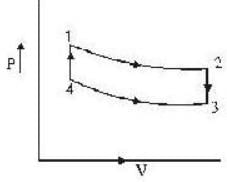
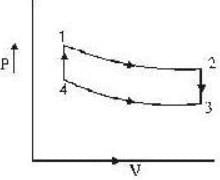
An ideal gas completes a cycle consisting of two isochores as shown in fig. Which one of the following are incorrect?
Which one among the following are false for Helmholtz free energy when the process is isothermal?
At higher temperature, which one of the following statement are false?
If the scalar function is f = x2 y z3 than at the point (2, 1,-1)
1 m3 of an ideal gas with v = 1.4 is at a pressure of 100 kPa and a temperature 300 K. Initially the state of the gas is at the point a of the PV diagram shown. The gas is taken through a reversible cycle a → b → c → a. The pressure at point b is 200 kPa and the line ba, when extended , passes through the origin.

The work done by the gas in each steps are  and
and  Calculate the value of n if
Calculate the value of n if

Two thermally isolated systems have heat capacities which vary as Cv = βT2 (where β > 0). Initially one system is at 300 K and the other at 600 K. The systems are then brought into thermal contact and the combined system is allowed to reach thermal equilibrium. Then calculate the final temperature (in Kelvin) of the combined system.
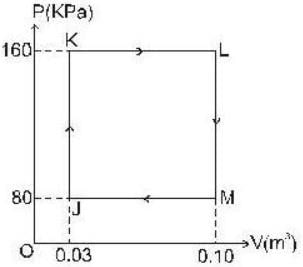
The P-V-diagram below represents an ideal monoatomic gas cycle for 1 mole of a gas. Calculate the work done (in Joule) during the cycle.
1 Kg of a liquid (specific heat = 2000 JK-1kg-1), independent of temperature, is heated from 300 K to 600 K by either of the following process P1 :
P1: bringing it in contact with a reservoir at 600 K.
Calculate the change in the entropy (in J/K) of the universe in process P1.
A carnot engine operating between two temperatures 727°C and 27°C is supplied heat energy at the rate of 500 joule/cycle. 60% of the work output is used to derive a refrigerator, which rejects heat to the surrounding at 27°C. If the refrigerator removes 1050 Joule of heat per cycle from the low temperature reservoir, determine the temperature (in Kelvin) of reservoir.
Consider a car not engine operating between temperatures of 800 and 400 k. The engine perform 2000 J of work per cycle. The heat extracted per cycle from the high temperature reservoir is_____
A given quantity of gas is taken from the state A → C reversibly, by two paths A → C directly and A → B → C as shown in the figure
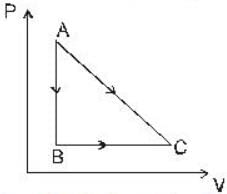
During the process A→ C the work done by the gas in 200J and the heat absorbed is 300 J. If during the porocess A → B → C the work done by the gas is 50J , the heat absorbed is____ .
30 gm of ice at 0°C is added to a beaker containing 60gm of water at 35°C. What is the final temperature of the system when it comes to internal equailibrium? (The specfic heat of water is 1 cal / gm°c and latent heat of melting of ice is 80 cal / gm)
find the rate of change of 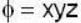 in the direction normal to the surface x2y + y1x+yz2 = 3 at the point (1,1,1)
in the direction normal to the surface x2y + y1x+yz2 = 3 at the point (1,1,1)
find the directional derivative of 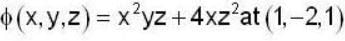 in the direction of
in the direction of 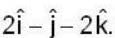 Find the the greatest rate of incrase of
Find the the greatest rate of incrase of 
|
4 docs|21 tests
|


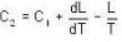

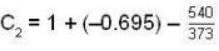
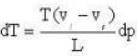
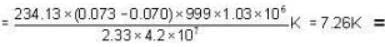 265 .740C
265 .740C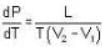
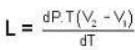
 3.39 * 109 ergs/gm.
3.39 * 109 ergs/gm. 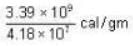
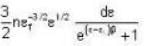

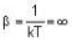
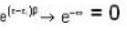
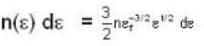
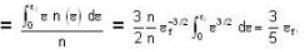
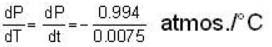
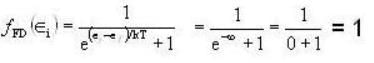
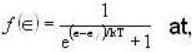 T = 0 K and
T = 0 K and 

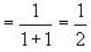

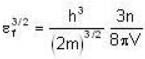


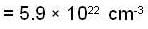
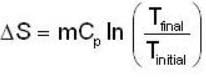
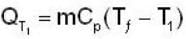
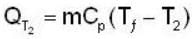

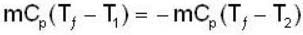
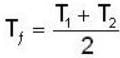
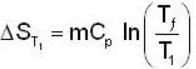
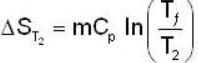
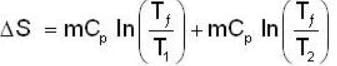

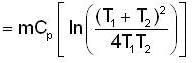
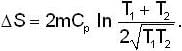
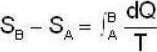
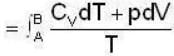
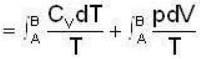
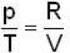
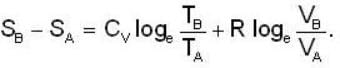
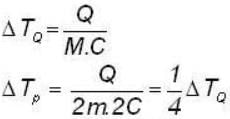
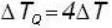
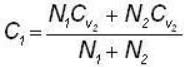
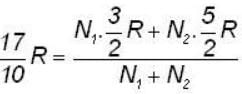
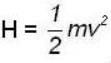

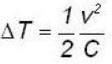
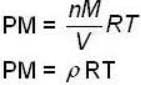
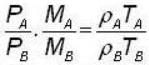
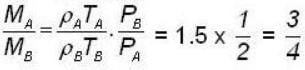
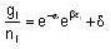
 for M.B
for M.B  for B.E
for B.E  for F.B and
for F.B and 
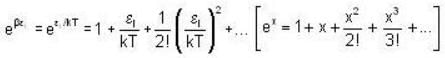
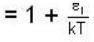
 and higher terms can be neglected.]
and higher terms can be neglected.]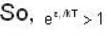
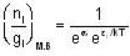 [Since, eα vary at higher temperature ]
[Since, eα vary at higher temperature ]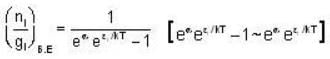 [factor T is neglected Since
[factor T is neglected Since 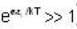 ]
]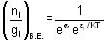
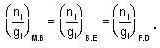
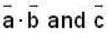 are unit vectors, then the value of
are unit vectors, then the value of 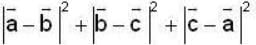 is possible
is possible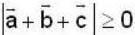
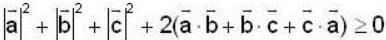
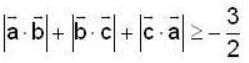
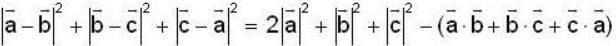
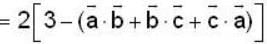
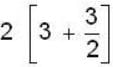
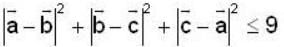
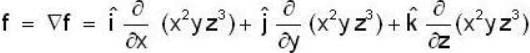
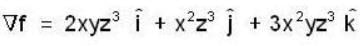
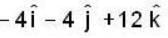
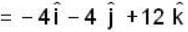
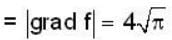

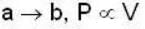

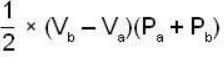
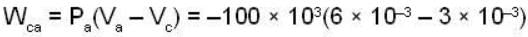
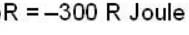
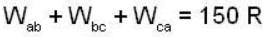

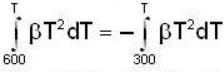


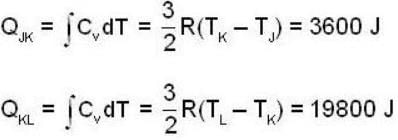
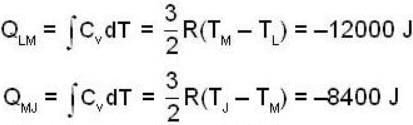
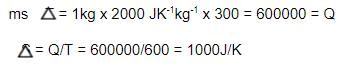
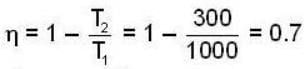

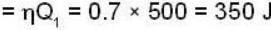
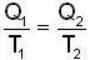
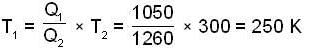
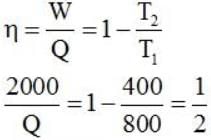
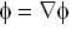
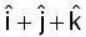
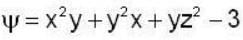
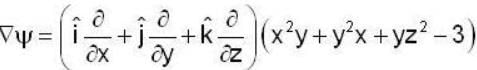
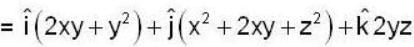
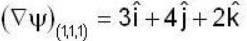
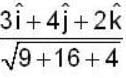
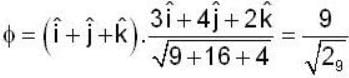
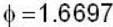
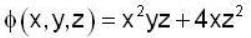
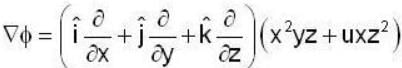
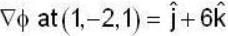
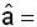 unit veetor =
unit veetor =