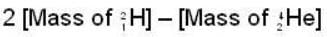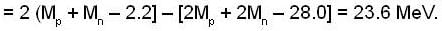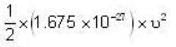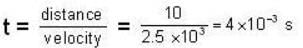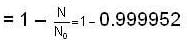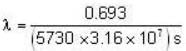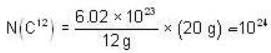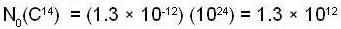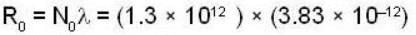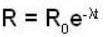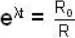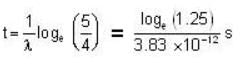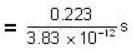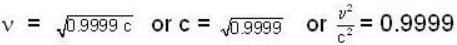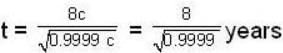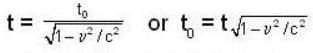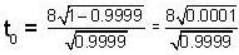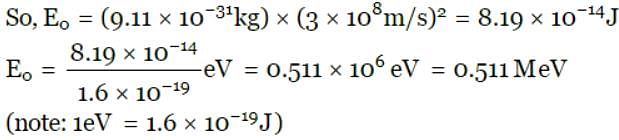IIT JAM Physics MCQ Test 9 - Physics MCQ
30 Questions MCQ Test IIT JAM Physics Mock Test Series 2025 - IIT JAM Physics MCQ Test 9
Calculate the percentage contraction of a rod moving with a velocity 0.8c in a direction inclined at 60o to its own length.
As measured by S a flashbulb goes off at x = 100 km, y = 10 km, z = 1 km at t = 0.5 ms. What are the coordinates x' y' z' and t’ of this event as determined by a second observer, S, moving relative to S at - 0 . 8 c along the common xx ’ axis?
The insignia painted on the side of spaceship is a circle with a line across it at 45° to the vertical. As the ship shoots past another ship in space, with a relative speed of 0.95c, the second ship observes the insignia. What angle does the observed line make to the vertical?
A thin rod has proper length I0. If the rod is moving at 0-6c is a direction at 30o to its own length, calculate its length and inclination.
Let two events A and B occur at two space points 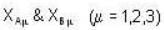 and difference vector be
and difference vector be 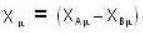 then the condition for xμ to be like space is
then the condition for xμ to be like space is
Rest mass energy of an election is 0. 51 MeV. A moving election has a kinetic energy of 9.69 MeV. The ratio of the mass of the moving electron to its mass is
Two particles are travelling in opposite directions with speed 0.9c relative to laboratory. Calculate their relative speed.
An astronaut moves in a super spaceship travelling at a speed of 0.8C. The astronaut observes a photon approaching him from space. The speed of photon with respect to the astronaut is
The power incident on a detector of light is 100 nW. Determine the number of photons per second incident on the detector if the wavelength is 800 nm.
What is the energy of a typical visible photon? About how many photons enter the eye per second when one looks at a weak source of light such as the moon, which produces light of intensity of about 3 * 10 -4 watts/m2?
In a photoelectric effect experiment, for radiation with frequency v0 with hv0 = 8 ev, electrons are emitted with energy 2 eV. What is the energy of the electrons emitted for incoming radiation of frequency 1.25 v0?
For the X-ray spectrum due to transition between n = 2 and n = 1 states for large nuclear charge Ze, we have frequencies 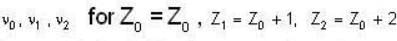 respectively . Mosley’s law implies which one of the following equations?
respectively . Mosley’s law implies which one of the following equations?
What is the uncertainty in the location of a photon of wavelength 3000 Å if this wavelength is known to an accuracy of one part in a million?
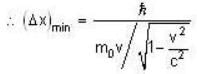
The least possible uncertainty in the position of an electron moving with velocity 2.8 x 109 cms -1 is
In the photoelectric effect, electromagnetic radiation is incident upon the surface of a metal. Which of the following are true statement about the photoelectric effect?
Which one of the following relations are false for Pauli matrices 
The matrices 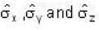 are called Paulis spin matrices, then which one of the relations are incorrect?
are called Paulis spin matrices, then which one of the relations are incorrect?
Consider the following statements and choose the correct answer
An o16 nucleus is spherical and has a charge radius R and a volume 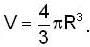 According to the empirical observations, the volume of 54 X128 nucleus assumed to be spherical is V ’ and radius R'. Then
According to the empirical observations, the volume of 54 X128 nucleus assumed to be spherical is V ’ and radius R'. Then
A μ- meson moves with a speed of 0.998 c and possesses an average lifetime of 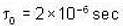 at rest, find the distance (in km) travelled by μ- meson, before decay? (Give the answer upto two decimal places)
at rest, find the distance (in km) travelled by μ- meson, before decay? (Give the answer upto two decimal places)
A man, who weighs 60 kg on earth, weighs 61 kg on a rocket, as measured by an observer on earth. What is the speed of the rocket?
One milliwatt of light of wavelength 4560 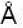 is incident on a cesium surface. Calculate the photoelectric current (in microampere) liberated assuming a quantum efficiency of 0.5%, given Planck’s constant h = 6.62 * 1O-34 J-s and velocity of light c = 3 * 108 m/sec.
is incident on a cesium surface. Calculate the photoelectric current (in microampere) liberated assuming a quantum efficiency of 0.5%, given Planck’s constant h = 6.62 * 1O-34 J-s and velocity of light c = 3 * 108 m/sec.
The wavelength of 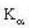 -line characteristic X-rays emitted by an element is 0.32
-line characteristic X-rays emitted by an element is 0.32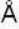 . The wavelength of
. The wavelength of 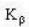 -line (in A°) emitted by the same element will be _______ .
-line (in A°) emitted by the same element will be _______ .
Find the energy release (in MeV), if two 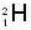 nuclei can fuse together to form 42He nucleus. The binding energy per nucleon of 2H and 4He is 1.1 meV and 7.0 MeV respectively.
nuclei can fuse together to form 42He nucleus. The binding energy per nucleon of 2H and 4He is 1.1 meV and 7.0 MeV respectively.
The binding energy of 17CI35 nucleus is 298 MeV. Find its atomic mass (in a.m.u.). The mass of hydrogen atom (1H1) is 1 -008143 a.m.u. and that of a neutron is 1.008986 a.m.u. Given 1 a.m.u. = 931 MeV.
There is a stream of neutrons with a kinetic energy of 0.0327 eV. If the half-life of neutrons is 700 seconds, what fraction of neutrons will decay before they travel a distance of 10m?
Given mass of neutron = 1.675 * 10-27 kg.
A piece of burnt wood of mass 20g is found to have a C14 activity of 4 decays/s. How long has the tree that this wood belonged to been dead (in years)?
Given T1/2 of C14 = 5730 years.
Find the time (in years) (as measured by clock at rest on a rocket) taken by a rocket to reach a distant star and return to the earth with a constant velocity
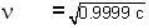
if the distant of the star is 4 light years.
Calculate the energy in MeV equivalent to the rest mass of an electron . Given that the rest mass of an electron, m = 9.1×10−31kg, 1MeV = 1.6×10−13J and speed of light , c = 3×108ms−1.
|
4 docs|21 tests
|



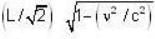 while the vertical extent is unchanged. Then
while the vertical extent is unchanged. Then
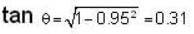
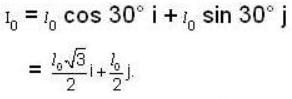
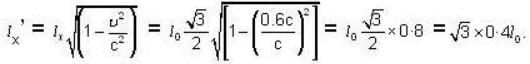

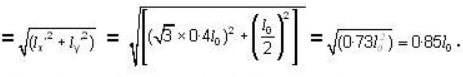
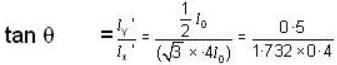
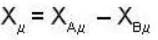
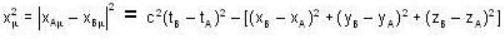
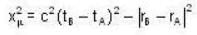
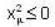
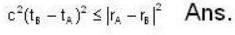
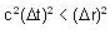 [for condition of like space]
[for condition of like space]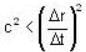
 Which is not possible.
Which is not possible.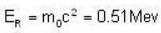
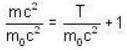
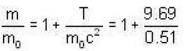
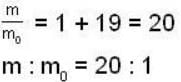
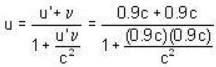
 because observed time
because observed time 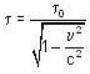 Where
Where 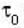 proper time interval.
proper time interval.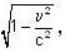 because observed length
because observed length 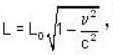 Where L0 is proper length.
Where L0 is proper length.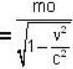 where mo is rest mass.
where mo is rest mass.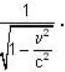
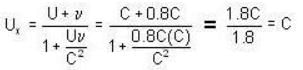


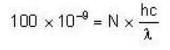
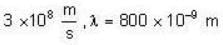
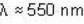 ...(i)
...(i)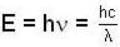 ...(ii)
...(ii)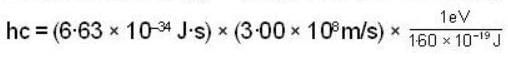
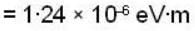
 ...(iv)
...(iv) and A is the area of the pupil
and A is the area of the pupil  if we take the diameter of the pupil to be about 6mm). Thus the number of photons entering our eye per second is number of photons per second
if we take the diameter of the pupil to be about 6mm). Thus the number of photons entering our eye per second is number of photons per second 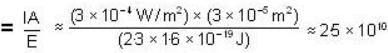 photons per second This is such a large number that the restriction to integer numbers of photons is quite unimportant even for this weak source.
photons per second This is such a large number that the restriction to integer numbers of photons is quite unimportant even for this weak source.
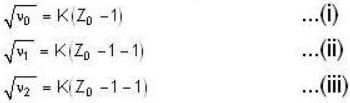

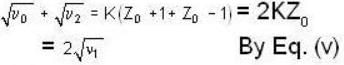
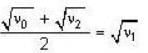
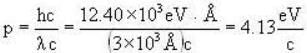
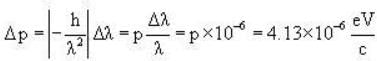
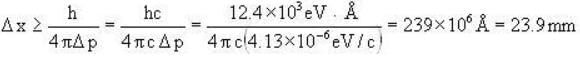
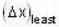 Axileaabe the least uncertainty in the position of the electron and
Axileaabe the least uncertainty in the position of the electron and 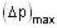 the maximum uncertainty in the momentum of the electron. Then
the maximum uncertainty in the momentum of the electron. Then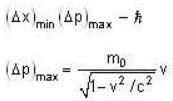


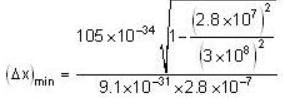 = 0.046 x 10-10 m = 0.046
= 0.046 x 10-10 m = 0.046
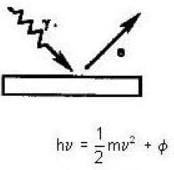
 is the work function of the metal. Furthermore,
is the work function of the metal. Furthermore,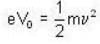
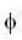 is the work function of the metal. Furthermore,
is the work function of the metal. Furthermore,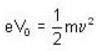
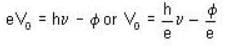

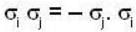
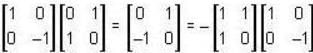
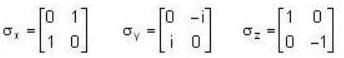
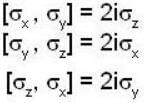
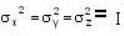
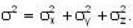
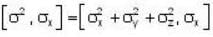
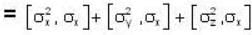
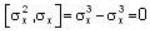
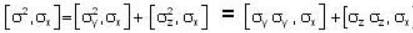 ]
]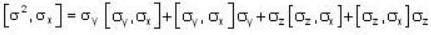
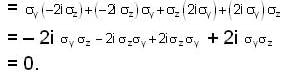
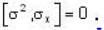
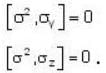
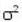 commutes with each component
commutes with each component 
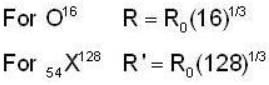
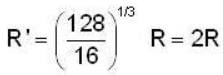
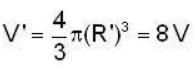

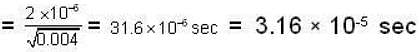
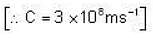
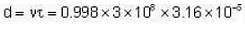

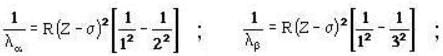
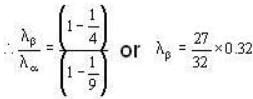
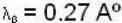
 nucleus is 4, hence B.E. for
nucleus is 4, hence B.E. for 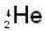 = 28.0 MeV, similarly B.E. for 2H nucleus (combination of one proton and one neutron) = 2.2 MeV.
= 28.0 MeV, similarly B.E. for 2H nucleus (combination of one proton and one neutron) = 2.2 MeV. nucleus = 2 [Mess of proton] + 2 [Mass of neutron) - 28.0 MeV.
nucleus = 2 [Mess of proton] + 2 [Mass of neutron) - 28.0 MeV.  nucleus = (Mass of proton) + [Mass of neutron) - 2.2 MeV.
nucleus = (Mass of proton) + [Mass of neutron) - 2.2 MeV.