JEE Advanced Level Test: Three Dimensional 3D Geometry- 2 - JEE MCQ
30 Questions MCQ Test - JEE Advanced Level Test: Three Dimensional 3D Geometry- 2
If the distance of the point P(1, -2, 1) from the plane x + 2y - 2z = a, where a > 0 is 5, then foot of perpendicular from P to the plane is
The image of point (3, -2, 1) in plane 3x – y + 4z = 2 is
The equation of plane passing through the point (0, 7, -7) and containing the line
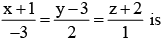
Let the line lie in the plane x + 3y - az + b = 0, then (a, b) equals
The angle between line and plane 3x – 2y + 6z = 0 is (m is scalar)
Let P(3, 2, 6) be a point in space and Q be a point on line Then value of m for which the vector
is parallel to the plane x-4y + 3z = 1 is
A variable plane at a distance of 1 unit from the origin cut the co-ordinate axis at A, B and C. If the centroid D (x, y, z) of ΔABC satisfy the relation then value of k is
The Cartesian equation of plane passing through (1, 1, 1) and containing the x-axis is
If the plane 2x – y + z = 0 is parallel to the line then value of a
is
Let L be the line of intersection of planes 2x + 3y + z = 1 and x + 3y + 2z = 2. If L makes an angle ‘α’ with the positive x-axis, then cosa equals
The ratio in which the line joining (2, 4, 5), (3, 5, -4) is divided by the yz-plane is
The equation of the plane through the point (-1, 2, 0) and parallel to the line
Equation of the line through (1, 1, 1) and perpendicular to the plane 2x + 3y – z – 5 = 0 is
Let A (1,1,1) , B (2, 3, 5) and C (-1, 0, 2) be three points, then equation of a plane parallel to the plane ABC which is a distance 2 is
The distance of the point (2, 1, -1) from the plane x - 2y + 4z = 9 is
A variable plane is at a constant distance 3p form the origin and meets the axes in A, B and C. The locus of the centroid of the triangle ABC is
The angle between the straight line and the plane 4x - 2y - 5z = 9
is
The distance between the line and the plane
Equation of the plane containing the straight line and perpendicular to the
plane containing the straight line
If the distance between the plane x - 2y + z = d and the plane containing the line
If the lines intersect, then k is equal to
A line with positive direction cosines passes through the point P(2, -1, 2) and makes equal angle with the coordinate axes. The line meets the plane 2x + y + z = 9 at point Q. The length of the line segment PQ equals
The d.r’s of the line AB are 6, - 2,9. If the line AB makes angles α,β with oy, oz respectively where O = ( 0, 0, 0) then sin2α - sin2β =
A line makes the same angle θ with each of the x - axis and z - axis. It makes β angle with y - axis such that sin2 β = 3sin2 θ then cos2 θ
If the angle θ between the line and plane
is such that
Then, value of λ is
A plane π passes through the point (1, 1, 1). If b, c, a are the direction ratios of a normal to the plane, where a, b, c ( a < b< c ) are the prime factors of 2001, then the equation of the plane π is
The point of intersection of the lines must be
The direction ratios of a normal to the plane through (1, 0, 0), (0, 1, 0) which makes an angle of with the plane x + y = 3 are
The equation of the plane passing through the mid-point of the line joining the points (1, 2, 3) and (3, 4, 5) and perpendicular to it is:



















