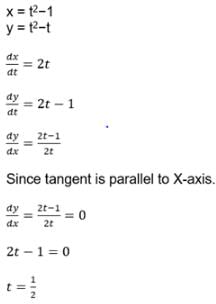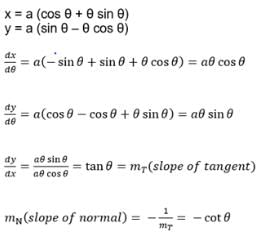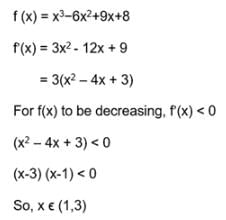Test: Application Of Derivatives - 2 - JEE MCQ
25 Questions MCQ Test - Test: Application Of Derivatives - 2
The function f (x) = x2 – 2 x is increasing in the interval
The function f (x) = a x + b is strict increasing for all x ∈ R iff
Tangents to the curve x2+y2 = 2at the points (1, 1) and (– 1, 1)
If x be real, the minimum value of x2−8x+17 is
If a differentiable function f (x) has a relative minimum at x = 0, then the function y = f (x) + a x + b has a relative minimum at x = 0 for
The function f (x) = a x + b is strict increasing for all x ∈ R if
Equation of the tangent to the curve at the point (a, b) is
a log | x | + bx2 + x has its extreme values at x = – 1 and x = 2, then
Let f (x) be differentiable in (0, 4) and f (2) = f (3) and S = {c : 2 < c < 3, f’ (c) = 0} then
The function f (x) = m x + c where m, c are constants, is a strict decreasing function for all x ∈ R if
The function f (x) = x2−2x is strict decreasing in the interval
The points on the curve 4 y = |x2−4| at which tangents are parallel to x – axis, are
For the curve x = t2−1,y = t2−t tangent is parallel to X – axis where
The slope of the normal to the curvex = a (cos θ + θ sin θ),y = a (sin θ – θ cos θ) at any point ‘θ’ is
Rolle’s Theorem is not applicable to the function f(x) = | x | for −2⩽x⩽2 because
Let f (x) = x3−6x2+9x+8, then f (x) is decreasing in
The equation of the normal to the curve y = sinx at (0, 0) is