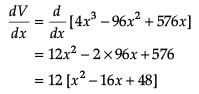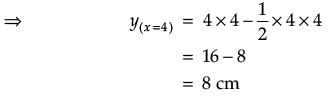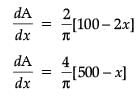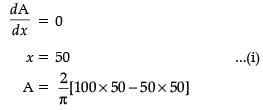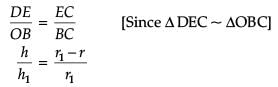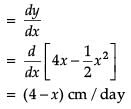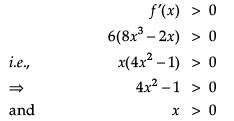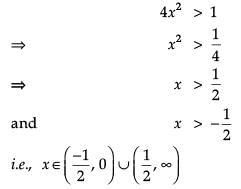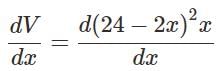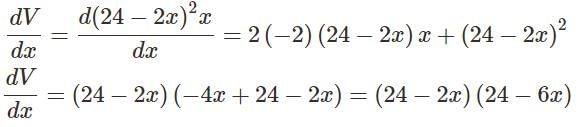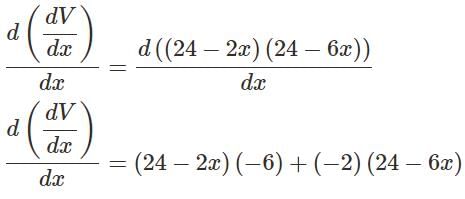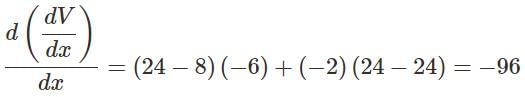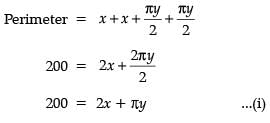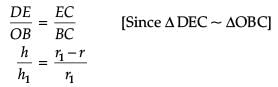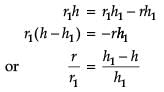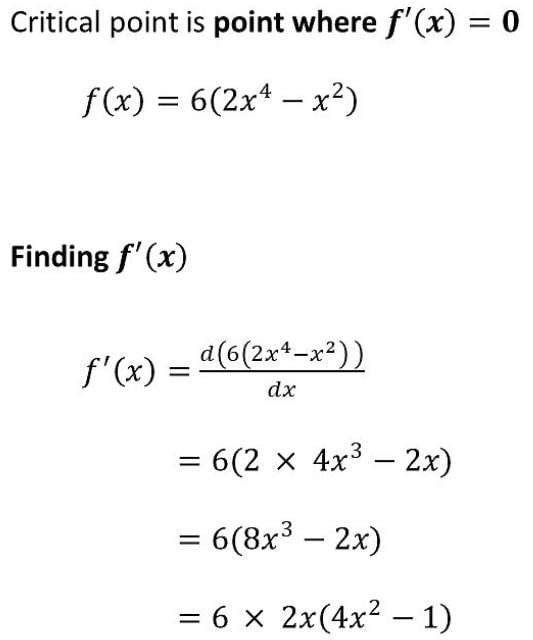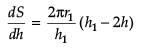Test: Application of Derivatives- Case Based Type Questions- 1 - JEE MCQ
15 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Application of Derivatives- Case Based Type Questions- 1
Read the following text and answer the following questions. On the basis of the same:
An open box is to be made out of a piece of cardboard measuring (24 cm × 24 cm) by cutting of equal squares from the corners and turning up the sides.
Find the value of dV/dx ?

Read the following text and answer the following questions, on the basis of the same:
The Relation between the height of the plant (y in cm) with respect to exposure to sunlight is governed by the following equation y = 4x – 1/2x2. where x is the number of days exposed to sunlight.

What is the maximum height of the plant?

| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Read the following text and answer the following questions on the basis of the same: The shape of a toy is given as f(x) = 6(2x4 – x2). To make the toy beautiful 2 sticks which are perpendicular to each other were placed at a point (2, 3), above the toy.

Find the second order derivative of the function at x = 5.

Read the following text and answer the following questions on the basis of the same:
P(x) = –5x2 + 125x + 37500 is the total profit function of a company, where x is the production of the company.

What will be the production when the profit is maximum?
Read the following text and answer the following questions, on the basis of the same:
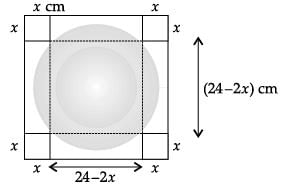
An architect designs a building for a multi-national company. The floor consists of a rectangular region with semicircular ends having a perimeter of 200 m as shown below:
The maximum value of area A is :
Read the following text and answer the following questions on the basis of the same:
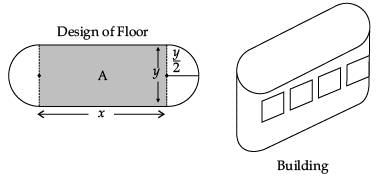
A right circular cylinder is inscribed in a cone.
S = Curved Surface Area of Cylinder.
r/r1 = ?
Read the following text and answer the following questions, on the basis of the same:
The Relation between the height of the plant (y in cm) with respect to exposure to sunlight is governed by the following equation y = 4x – 1/2x2. where x is the number of days exposed to sunlight.

The rate of growth of the plant with respect to sunlight is ______ .
Read the following text and answer the following questions on the basis of the same: The shape of a toy is given as f(x) = 6(2x4 – x2). To make the toy beautiful 2 sticks which are perpendicular to each other were placed at a point (2, 3), above the toy.

At which of the following intervals will f(x) be increasing?
Read the following text and answer the following questions. On the basis of the same:
An open box is to be made out of a piece of cardboard measuring (24 cm × 24 cm) by cutting of equal squares from the corners and turning up the sides.
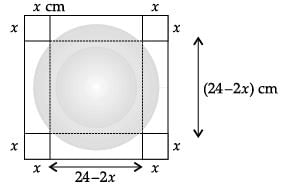
Find the value of x other than 12?
Read the following text and answer the following questions on the basis of the same:
P(x) = –5x2 + 125x + 37500 is the total profit function of a company, where x is the production of the company.

Check in which interval the profit is strictly increasing .
Read the following text and answer the following questions, on the basis of the same:
An architect designs a building for a multi-national company. The floor consists of a rectangular region with semicircular ends having a perimeter of 200 m as shown below:
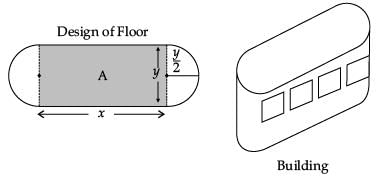
If x and y represents the length and breadth of the rectangular region, then the relation between the variables is :
Read the following text and answer the following questions on the basis of the same:
A right circular cylinder is inscribed in a cone.
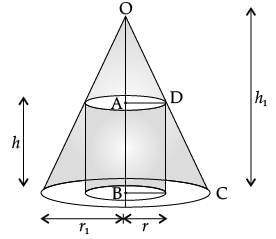
S = Curved Surface Area of Cylinder.
r/r1 = ?
Read the following text and answer the following questions on the basis of the same: The shape of a toy is given as f(x) = 6(2x4 – x2). To make the toy beautiful 2 sticks which are perpendicular to each other were placed at a point (2, 3), above the toy.

Which value from the following may be abscissa of critical point?
Read the following text and answer the following questions on the basis of the same:
A right circular cylinder is inscribed in a cone.
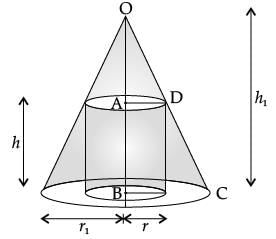
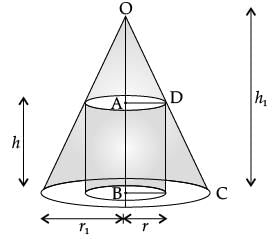
What is the value of dS/dh?
Read the following text and answer the following questions. On the basis of the same:
An open box is to be made out of a piece of cardboard measuring (24 cm × 24 cm) by cutting of equal squares from the corners and turning up the sides.

Volume is maximum at what height of that open box?
|
204 videos|290 docs|139 tests
|
|
204 videos|290 docs|139 tests
|