Test: Binary Operations - JEE MCQ
10 Questions MCQ Test - Test: Binary Operations
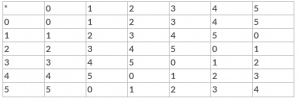
Given below is the table corresponding to some binary operation a * b on a set {0,1,2,3,4,5}. How many elements of this operation have an inverse?.
If * and O are two binary operations defined by a * b = a + b and a O b = ab, then
The number of binary operations which can be defined on the set P= {p, q} is
Given below is binary composition table a* b = LCM of a and b on S = {1,2,3,4}. Then, from the table determine which one of these options is correct.
Let * be any binary operation on the set R defined by a * b = a + b – ab, then the binary operation * is
Given below is the table corresponding to some binary operation a * b on a set {0, 1,2,3,4,5}. Identify the identity element of this operation.
The identity element for the binary operation * defined by a * b = ab/2, where a, b are the elements of a set of non-zero rational numbers, is



















