Test: Cartesian Equation Of A Line - JEE MCQ
10 Questions MCQ Test - Test: Cartesian Equation Of A Line
Let 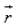 be the position vector of an arbitrary point P(x, y, z). Cartesian form of the equation of line passes through two points (x1, y1, z1) and (x2, y2, z2) is:
be the position vector of an arbitrary point P(x, y, z). Cartesian form of the equation of line passes through two points (x1, y1, z1) and (x2, y2, z2) is:
Find the vector equation of the line that passes through the origin and (-6,2,1).
The Cartesian equation of the line which passes through the point (2, -2, -1) and parallel to the line 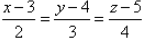 , is given by
, is given by
If the vector equation of a line is find its caryesian equation.
The vector form of the equation is. The Cartesian equation of the line is:
Let the coordinates of the given point A be (x1, y1, z1) and the direction ratios of the line be a, b, c. If the co-ordinates of any point P is (x, y, z), then the equation of the line in Cartesian form is:
Let be a position vector of A with respect to the origin O and
be a position vector of an arbitrary point. The equation of line which passes through A and parallel to a vector
is:
The Cartesian equation of the line passing through the points (-3, 1, 0) and (1, 2, 3) is:
The Cartesian equation of the line which passes through the origin and parallel to the line , is given by
Find the Cartesian equation of the line that passes through the point (-3,-4,-2) and (3,4,2).



















