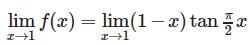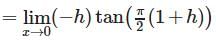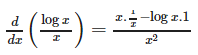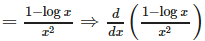Test: Continuity And Differentiability - 2 - JEE MCQ
25 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Continuity And Differentiability - 2
If f (x) is a polynomial of degree m (⩾1) , then which of the following is not true ?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let f and g be differentiable functions such that fog = I, the identity function. If g’ (a) = 2 and g (a) = b, then f ‘ (b) =
If f (x) =x2g(x) and g (x) is twice differentiable then f’’ (x) is equal to
Differential coefficient of a function f (g (x)) w.r.t. the function g (x) is
If y = aemx + be−mx, then y2 is equal to
If f(x) be any function which assumes only positive values and f’ (x) exists then f’ (x) is equal to
If y = a sin mx + b cos m x, then is equal to
If y = tan−1x and z = cot−1x then 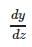 is equal to
is equal to
If both f and g are defined in a nhd of 0 ; f(0) = 0 = g(0) and f ‘ (0) = 8 = g’ (0), then equal to
The differential coefficient of log (| log x |) w.r.t. log x is
If f is derivable at x = a , then is equal to
|
204 videos|290 docs|139 tests
|
|
204 videos|290 docs|139 tests
|


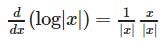
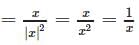


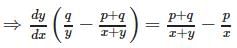
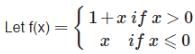
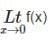 is equal to
is equal to