Test: Linear Programming (CBSE Level) - 2 - Commerce MCQ
25 Questions MCQ Test - Test: Linear Programming (CBSE Level) - 2
Let R be the feasible region (convex polygon) for a linear programming problem and let Z = ax + by be the objective function. When Z has an optimal value (maximum or minimum), where the variables x and y are subject to constraints described by linear inequalities,
Maximise Z = 3x + 4y subject to the constraints: x + y ≤ 4, x ≥ 0, y ≥ 0.
A factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines tomanufacture a package of screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacture a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of Rs 7 and screws B at a profit of Rs 10. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day in order to maximize his profit? Determine the maximum profit.
Determine the maximum value of Z = 11x + 7y subject to the constraints :2x + y ≤ 6, x ≤ 2, x ≥ 0, y ≥ 0.
The feasible region for a LPP is shown in Figure. Find the minimum value of Z = 11x + 7y.

Let R be the feasible region for a linear programming problem, and let Z = ax + by be the objective function. If R is bounded, then
Minimise Z = – 3x + 4 y subject to x + 2y ≤ 8, 3x + 2y ≤ 12, x ≥ 0, y ≥ 0.
A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of a grinding/cutting machine and a sprayer. It takes 2 hours on grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp. It takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at the most 20 hours and the grinding/cutting machine for at the most 12 hours. The profit from the sale of a lamp is Rs 5 and that from a shade is Rs 3. Assuming that the manufacturer can sell all the lamps and shades that he produces, how should he schedule his daily production in order to maximize his profit?
Maximize Z = 3x + 4y, subject to the constraints: x + y ≤ 1, x ≥ 0, y ≥ 0.
The feasible region for a LPP is shown in Figure. Find the maximum value of Z = 11x + 7y.

Let R be the feasible region for a linear programming problem,and let Z = ax + by be the objective function. If R is bounded, then the objective function Z has both a maximum and a minimum value on R and
Minimize Z = 3x + 5y such that x + 3y ≥ 3, x + y ≥ 2, x, y ≥ 0.
A company manufactures two types of novelty souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4hours for assembling. The profit is Rs 5 each for type A and Rs 6 each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize the profit?
Maximise the function Z = 11x + 7y, subject to the constraints: x ≤ 3, y ≤ 2,x ≥ 0, y ≥ 0.
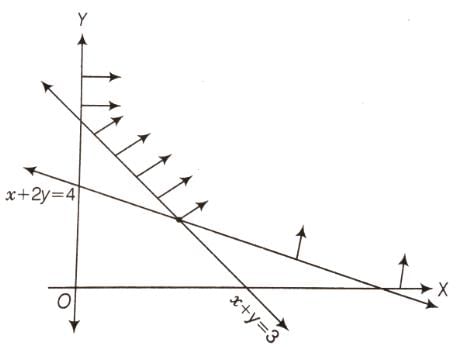
The feasible region for a LPP is shown in Figure. Evaluate Z = 4x + y at each of the corner points of this region. Find the minimum value of Z, if it exists
A maximum or a minimum may not exist for a linear programming problem if
Maximize Z = 3x + 2y subject to x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0.
A merchant plans to sell two types of personal computers – a desktop model and a portable model that will cost Rs 25000 and Rs 40000 respectively. He estimates that the total monthly demand of computers will not exceed 250 units. Determine the number of units of each type of computers which the merchant should stock to get maximum profit if he does not want to invest more than Rs 70 lakhs and if his profit on the desktop model is Rs 4500 and on portable model is Rs 5000.
Minimise Z = 13x – 15y subject to the constraints : x + y ≤ 7, 2x – 3y + 6 ≥ 0 , x ≥ 0, y ≥ 0.
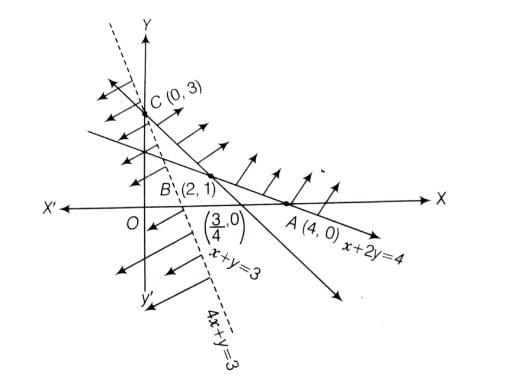
In Figure, the feasible region (shaded) for a LPP is shown. Determine the maximum and minimum value of Z = x + 2y
In Corner point method for solving a linear programming problem the first step is to
Minimize Z = x + 2y subject to 2x + y ≥ 3, x + 2y ≥ 6, x, y ≥ 0.
A diet is to contain at least 80 units of vitamin A and 100 units of minerals. Two foods F1 and F2 are available. Food F1 costs Rs 4 per unit food and F2 costs Rs 6 per unit. One unit of food F1 contains 3 units of vitamin A and 4 units of minerals. One unit of food F2 contains 6 units of vitamin A and 3 units of minerals. Formulate this as a linear programming problem. Find the minimum cost for diet that consists of mixture of these two foods and also meets the minimal nutritional requirements.
Maximize Z = 100x + 120y , subject to constraints 2x + 3y ≤ 30, 3x + y ≤ 17, x ≥ 0, y ≥ 0.
Determine the minimum value of Z = 3x + 4y if the feasible region (shaded) for a LPP is shown in Figure above.