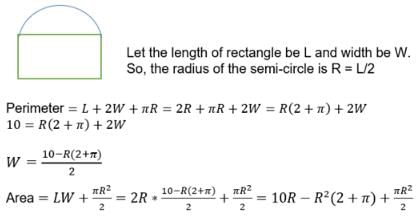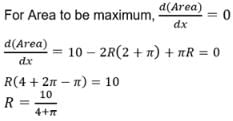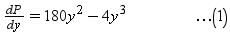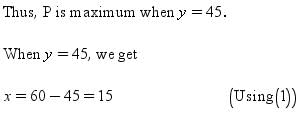Test: Maxima Minima (Derivative) - 2

I accept the Terms & Conditions.

Description

This mock test of Test: Maxima Minima (Derivative) - 2 for JEE helps you for every JEE entrance exam. This contains 10 Multiple Choice Questions for JEE Test: Maxima Minima (Derivative) - 2 (mcq) to study with solutions a complete question bank. The solved questions answers in this Test: Maxima Minima (Derivative) - 2 quiz give you a good mix of easy questions and tough questions. JEE students definitely take this Test: Maxima Minima (Derivative) - 2 exercise for a better result in the exam. You can find other Test: Maxima Minima (Derivative) - 2 extra questions, long questions & short questions for JEE on EduRev as well by searching above.

QUESTION: 1

A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 m. Find the radius of the semicircular opening of the window to admit maximum light.

Solution:

QUESTION: 2

The point of local maxima for the function f(x) = sinx. cos x is

A.
π/3
B.
π/2
C.
π/4
D.
π/6

Solution:

f(x) = sinx.cosx
f’(x) = -sin²x + cos²x
-sin²x + cos²x = 0
sin²x = cos²x
tan²x = 1
tanx = +-1
for tan x = 1, x = π/4
for tan x = -1, x = 3π/4
At x = π/4, f(π/4) = ½
At x = 3π/4, f(3π/4) = -½
At π/4 is the local maxima.

QUESTION: 3

A real number x when added to its reciprocal give minimum value to the sum when x is

A.
1/2
B.
-1
C.
1
D.
2

Solution:

QUESTION: 4

The sum of two positive numbers is 20. Find the numbers if their product is maximum

A.
5,15
B.
8,12
C.
20,0
D.
10,10

Solution:

QUESTION: 5

The function f(x) = log x

A.
Has a local maximum but no local minimum value
B.
Has both ,a local minimum and a local maximum value
C.
Has neither a local minimum nor a local maximum value
D.
Has a local minimum but no local maximum value

Solution:

f(x) = log x
f’(x) = 1/x
Putting f’(x) = 0
1/x = 0
x = ∞ (this is not defined for x)
So, f(x) does not have minima or maxima

QUESTION: 6

f(x) = x⁵ – 5x⁴ + 5x³ – 1. The local maxima of the function f(x) is at x =

A.
1
B.
5
C.
0
D.
3

Solution:

f(x) = x⁵ - 5x⁴ + 5x³ - 1
On differentiating w.r.t.x, we get
f'(x) = 5x⁴ - 20x³ + 15x²
For maxima or minima,f'(x) = 0
⇒ 5x⁴ - 20x³ + 15x² = 0
⇒ 5x²(x²-4x+3) = 0
⇒ 5x²(x-1)(x-3) = 0
⇒ x = 0,1,3
So, y has maxima at x = 1 and minima at x = 3
At x = 0, y has neither maxima nor minima, which is the point of inflection .
f(1) = 1-5+5-1=0,which is local maximum value at x = 1.

QUESTION: 7

How many units should be sold so that a company can make maximum profit if the profit function for x units is given by p(x) = 25 + 64x - x²

A.
16 units
B.
32 units
C.
8 units
D.
64 units

Solution:

QUESTION: 8

Find two numbers whose sum is 24 and product is a large as possible.

A.
12 and 12
B.
20 and 4
C.
8 and 16
D.
None of the above

Solution:

QUESTION: 9

A point c in the domain of a function f is called a critical point of f if

A.
f’ (x) = 0 at x = c
B.
f is not differentiable at x = c
C.
Either f’ (c) = 0 or f is not differentiable
D.
f” (x) = 0, at x = c

Solution:

A point C in the domain of a function f at which either f(c) = 0 or f is not differentiable.
The point f is called the critical point.
c is called the point of local maxima
If f ′(x) changes sign from positive to negative as x increases through c, that is, if f ′(x) > 0 at every point sufficiently close to and to the left of c, and f ′(x) < 0 at every point sufficiently close to and to the right of c.
c is called the point of local minima
If f ′(x) changes sign from negative to positive as x increases through c, that is, if f ′(x) < 0 at every point sufficiently close to and to the left of c, and f ′(x) > 0 at every point sufficiently close to and to the right of c.
c is called the point of inflexion
If f ′(x) does not change sign as x increases through c, then c is neither a point of local maxima nor a point of local minima.

QUESTION: 10

Find two positive numbers x and y such that x + y = 60 and xy³ is maximum

A.
x = 45, y = 15
B.
x = 15, y = 45
C.
x = 10, y = 50
D.
x = 30, y = 30

Solution:

two positive numbers x and y are such that x + y = 60.
x + y = 60
⇒ x = 60 – y ...(1)
Let P = xy³
∴ P =(60 – y)y³ = 60y³ – y4
Differentiating both sides with respect to y, we get

For maximum or minimum dP/dy = 0
⇒ 180y² - 4y³ = 0
⇒ 4y² (45 - y) = 0
⇒ y = 0 or 45 - y = 0
⇒ y = 0 or y = 45
⇒ y = 45 (∵ y = 0 is not possible)

Thus, the two positive numbers are 15 and 45.