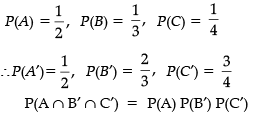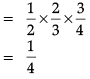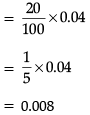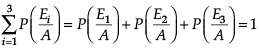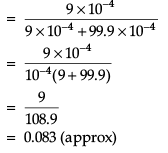Test: Probability- Case Based Type Questions- 1 - Commerce MCQ
15 Questions MCQ Test - Test: Probability- Case Based Type Questions- 1
Direction: Read the following text and answer the following questions on the basis of the same:
Anand, Samanyu and Shah of SHORTCUTS classes were given a problem in Mathematics whose respective probabilities of solving it are 1/2 , 1/3 and 1/4. They were asked to solve it independently.

Based on the above data, answer any four of the following questions.
Q. The probability that exactly one of them solves it is _______.

Direction: Read the following text and answer the following questions on the basis of the same:
Anand, Samanyu and Shah of SHORTCUTS classes were given a problem in Mathematics whose respective probabilities of solving it are 1/2 , 1/3 and 1/4. They were asked to solve it independently.

Based on the above data, answer any four of the following questions.
Q. The probability that the problem is not solved is _______.

Direction: Read the following text and answer the following questions on the basis of the same:
Anand, Samanyu and Shah of SHORTCUTS classes were given a problem in Mathematics whose respective probabilities of solving it are 1/2 , 1/3 and 1/4. They were asked to solve it independently.

Based on the above data, answer any four of the following questions.
Q. The probability that Anand alone solves it is _______.

Direction: Read the following text and answer the following questions on the basis of the same:
Anand, Samanyu and Shah of SHORTCUTS classes were given a problem in Mathematics whose respective probabilities of solving it are 1/2 , 1/3 and 1/4. They were asked to solve it independently.

Q. The probability that the problem is solved is _______.
Direction: Read the following text and answer the following questions on the basis of the same:
Anand, Samanyu and Shah of SHORTCUTS classes were given a problem in Mathematics whose respective probabilities of solving it are 1/2 , 1/3 and 1/4. They were asked to solve it independently.

Q. The probability that exactly two of them solves it is _______.
Direction: Read the following text and answer the following questions on the basis of the same:
In an office three employees Vinay, Sonia and Iqbal process incoming copies of a certain form. Vinay process 50% of the forms. Sonia processes 20% and Iqbal the remaining 30% of the forms. Vinay has an error rate of 0.06, Sonia has an error rate of 0.04 and Iqbal has an error rate of 0.03.

Q. The manager of the company wants to do a quality check. During inspection he selects a form at random from the days output of processed forms. If the form selected at random has an error, the probability that the form is NOT processed by Vinay is :
Direction: Read the following text and answer the following questions on the basis of the same:
In an office three employees Vinay, Sonia and Iqbal process incoming copies of a certain form. Vinay process 50% of the forms. Sonia processes 20% and Iqbal the remaining 30% of the forms. Vinay has an error rate of 0.06, Sonia has an error rate of 0.04 and Iqbal has an error rate of 0.03.

Q. The probability that Sonia processed the form and committed an error is :
Direction: Read the following text and answer the following questions on the basis of the same:
In an office three employees Vinay, Sonia and Iqbal process incoming copies of a certain form. Vinay process 50% of the forms. Sonia processes 20% and Iqbal the remaining 30% of the forms. Vinay has an error rate of 0.06, Sonia has an error rate of 0.04 and Iqbal has an error rate of 0.03.

Q. The conditional probability that an error is committed in processing given that Sonia processed the form is :
Direction: Read the following text and answer the following questions on the basis of the same:
In an office three employees Vinay, Sonia and Iqbal process incoming copies of a certain form. Vinay process 50% of the forms. Sonia processes 20% and Iqbal the remaining 30% of the forms. Vinay has an error rate of 0.06, Sonia has an error rate of 0.04 and Iqbal has an error rate of 0.03.

Q. The total probability of committing an error in processing the form is :
Direction: Read the following text and answer the following questions on the basis of the same:
In an office three employees Vinay, Sonia and Iqbal process incoming copies of a certain form. Vinay process 50% of the forms. Sonia processes 20% and Iqbal the remaining 30% of the forms. Vinay has an error rate of 0.06, Sonia has an error rate of 0.04 and Iqbal has an error rate of 0.03.

Q. Let A be the event of committing an error in processing the form and let E1, E2 and E3 be the events that Vinay, Sonia and Iqbal processed the form. The value of ![]()
Direction: Read the following text and answer the following questions on the basis of the same:
The reliability of a COVID PCR test is specified as follows:
Of people having COVID, 90% of the test detects the disease but 10% goes undetected. Of people free of COVID, 99% of the test is judged COVID negative but 1% are diagnosed as showing COVID positive. From a large population of which only 0.1% have COVID, one person is selected at random, given the COVID PCR test, and the pathologist reports him/ her as COVID positive.

Q. What is the probability that the ‘person is actually having COVID given that ‘he is tested as COVID positive’?
Direction: Read the following text and answer the following questions on the basis of the same:
The reliability of a COVID PCR test is specified as follows:
Of people having COVID, 90% of the test detects the disease but 10% goes undetected. Of people free of COVID, 99% of the test is judged COVID negative but 1% are diagnosed as showing COVID positive. From a large population of which only 0.1% have COVID, one person is selected at random, given the COVID PCR test, and the pathologist reports him/ her as COVID positive.

Q. What is the probability of the ‘person to be tested as COVID positive’ given that ‘he is actually not having COVID’?
Direction: Read the following text and answer the following questions on the basis of the same:
The reliability of a COVID PCR test is specified as follows:
Of people having COVID, 90% of the test detects the disease but 10% goes undetected. Of people free of COVID, 99% of the test is judged COVID negative but 1% are diagnosed as showing COVID positive. From a large population of which only 0.1% have COVID, one person is selected at random, given the COVID PCR test, and the pathologist reports him/ her as COVID positive.

Q. What is the probability of the ‘person to be tested as COVID positive’ given that ‘he is actually having COVID’?
Direction: Read the following text and answer the following questions on the basis of the same:
The reliability of a COVID PCR test is specified as follows:
Of people having COVID, 90% of the test detects the disease but 10% goes undetected. Of people free of COVID, 99% of the test is judged COVID negative but 1% are diagnosed as showing COVID positive. From a large population of which only 0.1% have COVID, one person is selected at random, given the COVID PCR test, and the pathologist reports him/ her as COVID positive.

Q. What is the probability that the ‘person is actually not having COVID’?
Direction: Read the following text and answer the following questions on the basis of the same:
The reliability of a COVID PCR test is specified as follows:
Of people having COVID, 90% of the test detects the disease but 10% goes undetected. Of people free of COVID, 99% of the test is judged COVID negative but 1% are diagnosed as showing COVID positive. From a large population of which only 0.1% have COVID, one person is selected at random, given the COVID PCR test, and the pathologist reports him/ her as COVID positive.

Q. What is the probability that the ‘person selected will be diagnosed as COVID positive’?