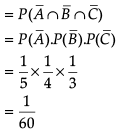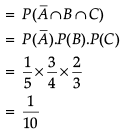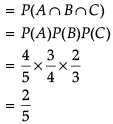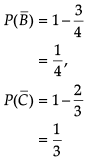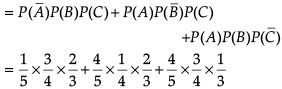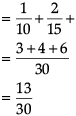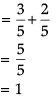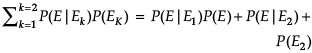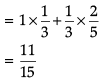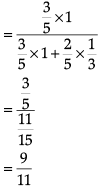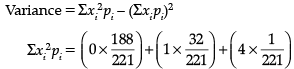Test: Probability- Case Based Type Questions- 2 - JEE MCQ
15 Questions MCQ Test Mathematics (Maths) Class 12 - Test: Probability- Case Based Type Questions- 2
Direction: Read the following text and answer the following questions on the basis of the same:
A coach is training 3 players. He observes that the player A can hit a target 4 times in 5 shots, player B can hit 3 times in 4 shots and the player C can hit 2 times in 3 shots.
Q. What is the probability that ‘none of them will hit the target’?
Direction: Read the following text and answer the following questions on the basis of the same:
A coach is training 3 players. He observes that player A can hit a target 4 times in 5 shots, player B can hit 3 times in 4 shots and player C can hit 2 times in 3 shots.
Q. What is the probability that B, C will hit and A will lose?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Direction: Read the following text and answer the following questions on the basis of the same:
A coach is training 3 players. He observes that player A can hit a target 4 times in 5 shots, player B can hit 3 times in 4 shots and player C can hit 2 times in 3 shots.
Q. Let the target is hit by A, B: the target is hit by B and, C: the target is hit by A and C. Then, the probability that A, B and, C all will hit, is
Direction: Read the following text and answer the following questions on the basis of the same:
A coach is training 3 players. He observes that player A can hit a target 4 times in 5 shots, player B can hit 3 times in 4 shots and the player C can hit 2 times in 3 shots.
Q. What is the probability that ‘any two of A, B and C will hit?
Direction: Read the following text and answer the following questions on the basis of the same:
A coach is training 3 players. He observes that player A can hit a target 4 times in 5 shots, player B can hit 3 times in 4 shots and the player C can hit 2 times in 3 shots.
Q. What is the probability that at least one of A, B or C will hit the target?
Direction: Read the following text and answer the following questions on the basis of the same:
In answering a question on a multiple choice test for class XII, a student either knows the answer or guesses. Let 3/5 be the probability that he knows the answer and 2/5 be the probability that he guesses. Assume that a student who guesses at the answer will be correct with probability 1/3. Let E1, E2, E be the events that the student knows the answer, guesses the answer and answers correctly respectively.
Q. 
Direction: Read the following text and answer the following questions on the basis of the same:
In answering a question on a multiple choice test for class XII, a student either knows the answer or guesses. Let 3/5 be the probability that he knows the answer and 2/5 be the probability that he guesses. Assume that a student who guesses at the answer will be correct with probability 1/3. Let E1, E2, E be the events that the student knows the answer, guesses the answer and answers correctly respectively.
Q. Value of P(E|E1) is
Direction: Read the following text and answer the following questions on the basis of the same:
In answering a question on a multiple choice test for class XII, a student either knows the answer or guesses. Let 3/5 be the probability that he knows the answer and 2/5 be the probability that he guesses. Assume that a student who guesses at the answer will be correct with probability 1/3. Let E1, E2, E be the events that the student knows the answer, guesses the answer and answers correctly respectively.
Q. What is the value of P(E1)?
Direction: Read the following text and answer the following questions on the basis of the same:
In answering a question on a multiple choice test for class XII, a student either knows the answer or guesses. Let 3/5 be the probability that he knows the answer and 2/5 be the probability that he guesses. Assume that a student who guesses at the answer will be correct with probability 1/3. Let E1, E2, E be the events that the student knows the answer, guesses the answer and answers correctly respectively.
Q. 
Direction: Read the following text and answer the following questions on the basis of the same:
In answering a question on a multiple choice test for class XII, a student either knows the answer or guesses. Let 3/5 be the probability that he knows the answer and 2/5 be the probability that he guesses. Assume that a student who guesses at the answer will be correct with probability 1/3. Let E1, E2, E be the events that the student knows the answer, guesses the answer and answers correctly respectively.
Q. What is the probability that the student knows the answer given that he answered it correctly?
Direction: Read the following text and answer the following questions on the basis of the same:
A group of people start playing cards. And as we know a well shuffled pack of cards contains a total of 52 cards. Then 2 cards are drawn simultaneously (or successively without replacement).
Q. Find the mean of the number of kings ?
Direction: Read the following text and answer the following questions on the basis of the same:
A group of people start playing cards. And as we know a well shuffled pack of cards contains a total of 52 cards. Then 2 cards are drawn simultaneously (or successively without replacement).
Q. If x = no. of kings = 0, 1, 2. Then P(x = 1) = ?
Direction: Read the following text and answer the following questions on the basis of the same:
A group of people start playing cards. And as we know a well shuffled pack of cards contains a total of 52 cards. Then 2 cards are drawn simultaneously (or successively without replacement).
Q. If x = no. of kings = 0, 1, 2. Then P(x = 0) = ?
Direction: Read the following text and answer the following questions on the basis of the same:
A group of people start playing cards. And as we know a well shuffled pack of cards contains a total of 52 cards. Then 2 cards are drawn simultaneously (or successively without replacement).
Q. If x = no. of kings = 0, 1, 2. Then P(x = 2) = ?
Direction: Read the following text and answer the following questions on the basis of the same:
A group of people start playing cards. And as we know a well shuffled pack of cards contains a total of 52 cards. Then 2 cards are drawn simultaneously (or successively without replacement).
Q. Find the variance of the number of kings ?
|
204 videos|290 docs|139 tests
|
|
204 videos|290 docs|139 tests
|
Top Courses for JEE
Important Questions for Probability- Case Based Type Questions- 2
Probability- Case Based Type Questions- 2 MCQs with Answers
Online Tests for Probability- Case Based Type Questions- 2 Mathematics (Maths) Class 12
|
© EduRev
|
Education Revolution
|
|
