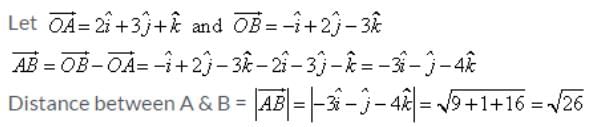Test: Properties Of Vectors - JEE MCQ
Test Description
10 Questions MCQ Test - Test: Properties Of Vectors
Test: Properties Of Vectors for JEE 2025 is part of JEE preparation. The Test: Properties Of Vectors questions and answers have been prepared
according to the JEE exam syllabus.The Test: Properties Of Vectors MCQs are made for JEE 2025 Exam.
Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Properties Of Vectors below.
Solutions of Test: Properties Of Vectors questions in English are available as part of our course for JEE & Test: Properties Of Vectors solutions in
Hindi for JEE course.
Download more important topics, notes, lectures and mock test series for JEE Exam by signing up for free. Attempt Test: Properties Of Vectors | 10 questions in 10 minutes | Mock test for JEE preparation | Free important questions MCQ to study for JEE Exam | Download free PDF with solutions
Test: Properties Of Vectors - Question 1
Any vector in an arbitrary direction can be replaced by two or three vectors
Detailed Solution for Test: Properties Of Vectors - Question 1
Test: Properties Of Vectors - Question 2
The position vector of mid-point of joining the points (2, – 1, 3) and (4, 3, –5) is :
Detailed Solution for Test: Properties Of Vectors - Question 2
Test: Properties Of Vectors - Question 3
The Position vector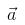 of a point (12,n) is such that
of a point (12,n) is such that 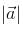 = 13 then n =
= 13 then n =
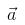 of a point (12,n) is such that
of a point (12,n) is such that 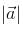 = 13 then n =
= 13 then n =
Detailed Solution for Test: Properties Of Vectors - Question 3
Test: Properties Of Vectors - Question 4
The vector joining the points A(2, – 3, 1) and B(1, – 2, – 5) directed from B to A is:
Detailed Solution for Test: Properties Of Vectors - Question 4
Test: Properties Of Vectors - Question 5
ABCD is a parallelogram. If coordinates of A,B,C are (2,3), (1,4) and (0, -2). Coordinates of D =
Detailed Solution for Test: Properties Of Vectors - Question 5
Test: Properties Of Vectors - Question 6
The position vectors of the end points of diameter of a circle are and
, then the position vector of the centre of the circle is:
Detailed Solution for Test: Properties Of Vectors - Question 6
Detailed Solution for Test: Properties Of Vectors - Question 7
Test: Properties Of Vectors - Question 8
The points with position vectors are collinear vectors, Value of a =
Detailed Solution for Test: Properties Of Vectors - Question 8
Test: Properties Of Vectors - Question 9
The distance between the point (2, 3, 1) and (–1, 2, – 3) is:
Detailed Solution for Test: Properties Of Vectors - Question 9
Detailed Solution for Test: Properties Of Vectors - Question 10
Information about Test: Properties Of Vectors Page
In this test you can find the Exam questions for Test: Properties Of Vectors solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Properties Of Vectors , EduRev gives you an ample number of Online tests for practice
Download as PDF