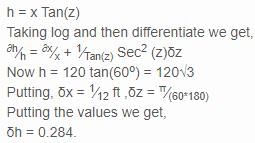Test: Rate of Change And Approximations - JEE MCQ
10 Questions MCQ Test - Test: Rate of Change And Approximations
The radius of air bubble is increasing at the rate of 0. 25 cm/s. At what rate the volume of the bubble is increasing when the radius is 1 cm.
The total revenue in Rupees received from the sale of x units of a product is given by R(x) = 5x2 + 22x + 35. Find the marginal revenue, when x = 7, where by marginal revenue we mean the rate of change of total revenue with respect to the number of items sold at an instant
Find the approximate change in total surface area of a cube of side x metre caused by increase in side by 1%.
The volume of cube is increasing at the constant rate of 3 cm3/s. Find the rate of change of edge of the cube when its edge is 5 cm.
The total cost associated with the production of x units of a product is given by C(x) = 5x2 + 14x + 6. Find marginal cost when 5 units are produced
At a distance of 120ft from the foot of a tower the elevation of its top is 60o. If the possible error in measuring the distance and elevation are 1 inch and 1 minute, find approximate error in calculated height.
A stone is dropped into a quiet lake and waves move in circles at a speed of 2cm per second. At the instant, when the radius of the circular wave is 12 cm, how fast is the enclosed area changing ?
Find the approximate value of f(10.01) where f(x) = 5x2 +6x + 3
Given a function y = f(x) . Let Δx be the very small change in the value of x , then the corresponding change in the value of y that is Δy is approximately given by