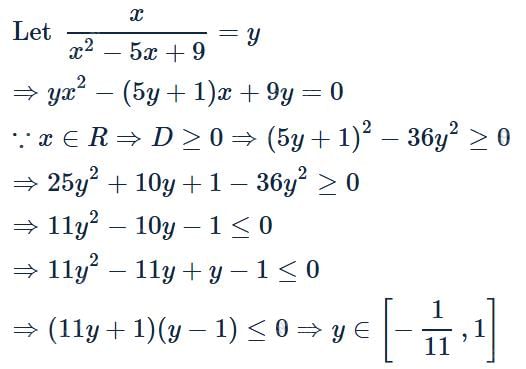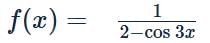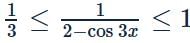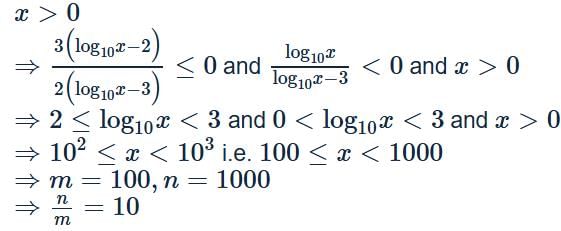Test: Relations & Functions- 1 - JEE MCQ
25 Questions MCQ Test - Test: Relations & Functions- 1
Let R be the relation over the set of straight lines of a plane such that l1 R l2 ⇔ l1 ⊥ l2. Then, R is
The binary relation S = Φ (empty set) on set A = {1, 2, 3} is
The void relation (a subset of A x A) on a non empty set A is:
The domain of the function f = {(1, 3), (3, 5), (2, 6)} is
Let R be the relation on N defined as x R y if x + 2 y = 8. The domain of R is
If A = {1, 2, 3}, then the relation R = {(1, 2), (2, 3), (1, 3) in A is
If f: (0, π) → R is given by (x)=∑nk=1 [1 + sin kx], [x] denotes the greatest integer function, then the range of f(x) is
Let A = {a, b, c} and R = {(a, a), (b, b), (c, c), (b, c)} be a relation on A. Here, R is
Let f(x) = x4 − 2x2 + 5 be defined on [−2, 2]
Statement-1: The range of f(x) is [2,13]
Statement-2: The greatest value of f is attained at x = 2
A relation R from C to R is defined by x Ry iff |x| = y. Which of the following is correct?
A relation R in a set A is said to be an equivalence relation if
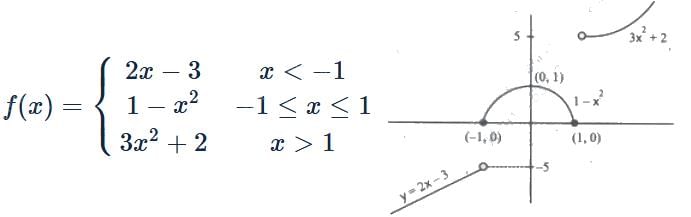
Let f: R → R be a mapping such that f(x) = 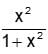 . Then f is
. Then f is
If f:R → R and is defined by  for each x ∈ R, then the range of f is
for each x ∈ R, then the range of f is
If (m, n) represents the domain of the function defined as 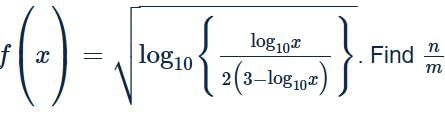


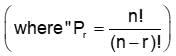

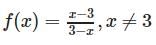 is
is 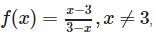
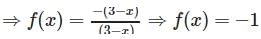
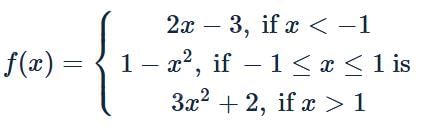
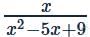 is
is