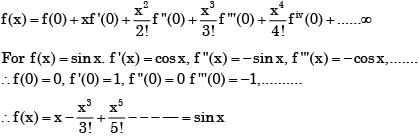Test: Fourier Series - Mathematics MCQ
20 Questions MCQ Test Calculus - Test: Fourier Series
Choose the function f(t); –∞ < t < ∞, for which a Fourier series cannot be defined.
The Fourier series of a real periodic function has only
P. cosine terms if it is even
Q. sine terms if it is even
R. cosine terms if it is odd
S. sine terms if it is odd
Q. Which of the above statements are correct?
P. cosine terms if it is even
Q. sine terms if it is even
R. cosine terms if it is odd
S. sine terms if it is odd
Q. Which of the above statements are correct?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
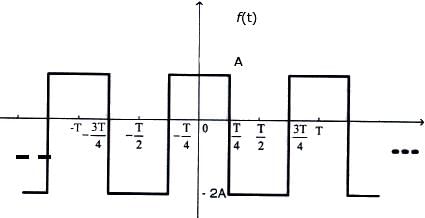
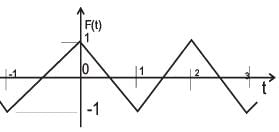
The trigonometric Fourier series for the waveform f(t) shown below contains

For the function e-x, the linear approximation around x = 2 is
Which of the following functions would have only odd powers of x in its Taylor series expansion about the point x = 0?
In the Taylor series expansion of exp(x) + sin(x) about the point x = π, the coefficient of (x – π)2 is
The function x(t) is shown in the figure. Even and odd parts of a unit-step function u(t) are respectively,

For x = π/6, the sum of series  (cos x)2n = cos2x + cos4x + ......is
(cos x)2n = cos2x + cos4x + ......is
In the Taylor series expansion of ex about x = 2, the coefficient of (x-2)4 is
The Fourier series expansion of a symmetric and even function, f(x) where
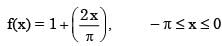
And 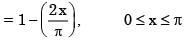
Will be
The Fourier series expansion 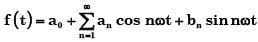 of the periodic signal shown below will contain the following nonzero terms
of the periodic signal shown below will contain the following nonzero terms
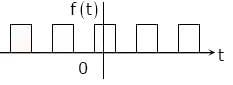
X(t) is a real valued function of a real variable with period T. Its trigonometric Fourier Series expansion contains no terms of frequency ω = 2π (2k ) / T ; k = 1, 2,.... Also, no sine terms are present. Then x(t) satisfies the equation
The Fourier Series coefficients, of a periodic signal x(t), expressed as
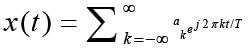
are given by 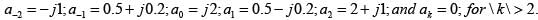
Witch of the following is true?
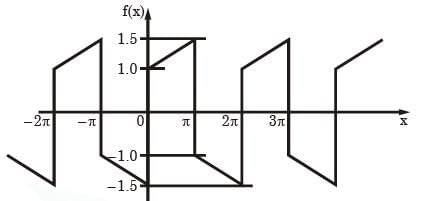
f(x), shown in the figure is represented by f(x) = 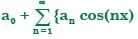 + bn sin(nx)}. The value of a0 is
+ bn sin(nx)}. The value of a0 is
Given the discrete-time sequence x[b] = [2,0,-1,-3,4,1,-1], x(ejπ) is
|
112 videos|65 docs|3 tests
|



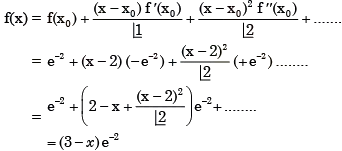
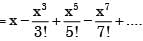

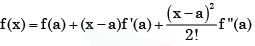
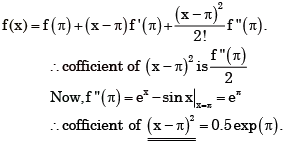
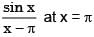 is given by
is given by 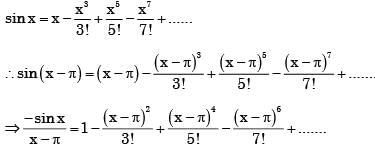
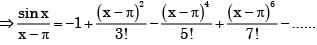
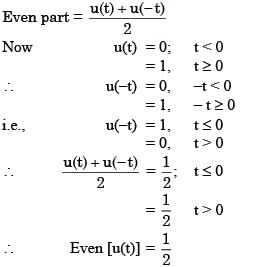
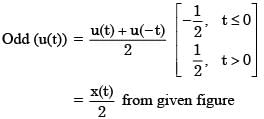
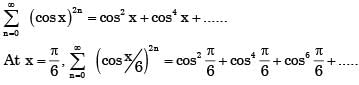
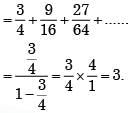
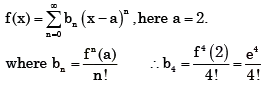
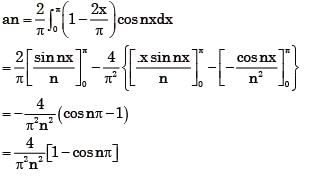
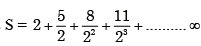 is
is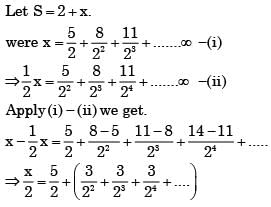
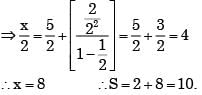
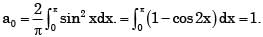 we know
we know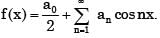
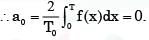
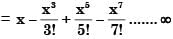 converges to
converges to