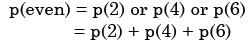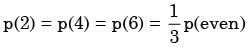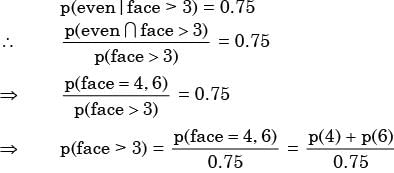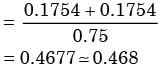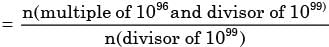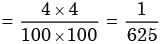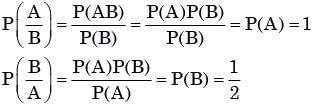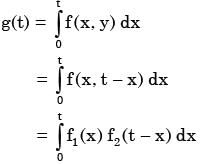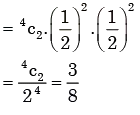Test: Statistics Part:- 2 - Mathematics MCQ
10 Questions MCQ Test Additional Topics for IIT JAM Mathematics - Test: Statistics Part:- 2
Suppose we uniformly and randomly select a permutation from the 20! permutations of 1, 2, 3 ….., 20. What is the probability that 2 appears at an earlier position that any other even number in the selected permutation?
Aishwarya studies either computer science or mathematics everyday. if the studies computer science on a day, then the probability that she studies mathematics the next day is 0.6. If she studies mathematics on a day, then the probability that she studies computer science the next day is 0.4. Given that Aishwarya studies computer science on Monday, what is the probability that she studies computer science on Wednesday?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let X be a randon variable following normal distribution with mean +1 and variance 4. Let Y be another normal variable with mean –1 and variance unknown. If P(X ≤ –1) = P(Y ≥ 2) the standard deviation of Y is
An unbalanced ice (with 6 faces, numbered from 1 to 6) is thrown. The probability that the face value is odd is 90% of the probability that the face value is even. The probability of getting any even numbered face is the same.
If the probability that the face is even given that it is greater than 3 is 0.75, which one of the following options is closed to the probability that the face value exceeds 3?
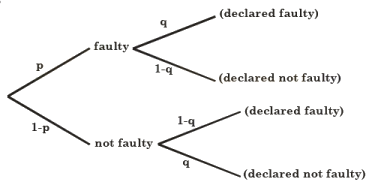
Consider a company that assembles computers. The probability of a faulty assembly of any computer is p. The company, therefore, subjects each computer to a testing process. This testing process gives the correct result for any computer with a probability of q.
What is the probability of a computer being declared faulty?
What is the probability that a divisor of 1099 is a multiple of 1096?
Let P(E) denote the probability of the even E. Given P(A) = 1, P(B) = 1/2, the values of P(A/B) and p(B/A) respectively are
A program consists of two modules executed sequentially. Let f1 (t) and f2 (t) respectively denote the probability density functions of time taken to execute the two modules. The probability density function of the overall time taken to execute the program is given by
If a fair coin is tossed four times. What is the probability that two heads and two tails will result?
An examination paper has 150 multiple-choice questions of one mark each, with each question having four choices. Each incorrect answer fetches – 0.25 mark. Suppose 1000 students choose all their answers randomly with uniform probability. The sum total of the expected marks obtained all these students is


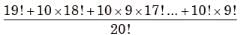
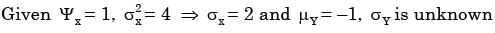
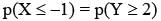
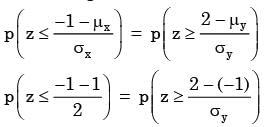
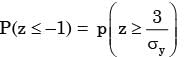 ...(i)
...(i)