Test: Group Theory - 10 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Group Theory - 10
The order of the permutation (12) (546) (3978) in the symmetric group S9 is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let S1 = {2 }, S2 = {4, 6}, S3 = {8, 10,12,} S4 = {14 ,16 , 18, 20 } and so on. The sum of elements of S10 is
Let x * y = 3xy for all x , y ε R\{ 0 } . The inverse o f the element 2 in the group (R\{0}, *) is
Let G be a group with identity e such that for some a ε G, a2 ≠ e and a6 = e. Then which of the following is true?
The number of subsets of { 1 , 2 , . . . , 10} which are disj oint from {3, 7, 8} is
Let P be a set having n > 10 elements. The number of subsets of P having odd number of elements is
Consider the set {1, 3, 7, 9} under the operation of multiplication modulo 10. Which one of the 4following statements about the given set is FALSE?
Let S be a set with 10 elements. The number of subsets of S having odd number of elements is
The total number of non-trivial proper subgroups of the group Z12 under addition modulo 12 is
Let F be a field with five elements and let K={{a, b) | a, b ε F} with the binary operations defined componentwise. Then
Let X= {1,2, 3,4}. Then the total number of partition of the set X is
If a = (13)(254) in the symmetric group S5 then α65 equals
For a, b ε Z, define a relation a R b if ab ≥ 0. Then the relation R is
Let R be a commutative ring with unity of characteristic 3, For a, b ε R, (a + b)6 is equal to
A non empty set A is termed as an algebraic structure ________
|
27 docs|150 tests
|


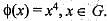 Then φ is
Then φ is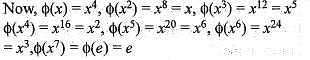
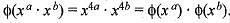
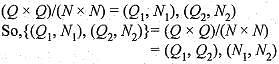
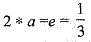 implies 3 x 2 x a = 1/3, So, a = 1/18.
implies 3 x 2 x a = 1/3, So, a = 1/18. 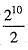 = 512
= 512