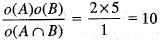Test: Group Theory - 7 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Group Theory - 7
If H is a subgroup of G, then number of left cosets of H in G and number of right cosets of H in G are
If F is homomorphism of a group G into a group G' with kernal K, then
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If G is a finite group and II is a normal subgroup of G, then 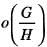 is
is
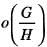 is
isLet G be a group of order 15. Then the number of sylow subgroup of G of order 3 is
Choose the correct answer. If His a normal subgroup of G and K is a normal subgroup of H, then
Let G and H be two groups. The groups G x H and H x G are isomorphic
Let l be the additive group of integers. Let H = {3x/x ⊂ l} normal subgroup of l, the elements of l/H are
If H and K are two subgroups of G of order 6 and 8, then order of HK is 16 if
If G is a group of order 10 then G have a subgroup of order
Let the set Z/ nZ denote the ring of integers modulo n under addition and multiplication modulo n then, Z/ 9Z is not a subring of Z/12Z because
If a and a2 are both generators of a cycle group of order m, then
If a and a2 both are generator of a cyclic group, then the order of the group gcd(2, n) = 1⇒ n = odd positive integer > 1
Let G be a cyclic group of order 6, Then, the number of element g ∈ G such that G = (g) is
Let S be a set and P(S) be the power set of S. Then {P(S), U} is not a group because
Let G be a group of order 30. Let A and B be normal subgroup of order 2 and 5, respectively. Then the order o f the group G / AB is
|
27 docs|150 tests
|


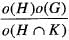

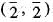 in Z4 x Z6 is
in Z4 x Z6 is