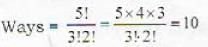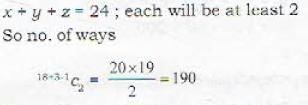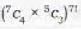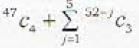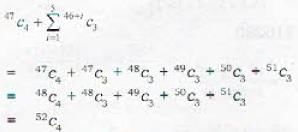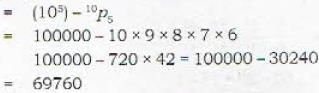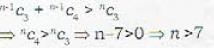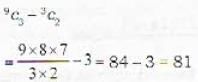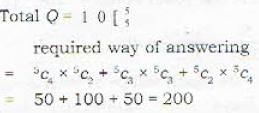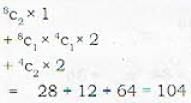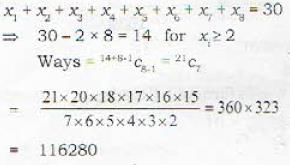Test:- Permutations And Combinations - 7 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test:- Permutations And Combinations - 7
The number of 5 letters words that can be formed containing at least one vowel is
The number of different message that can be represented by sequence of three dashes and two dots is :
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The number of intergeral solution of the equation x + y + z = 24 in which each integer is greater than 1 is:
If nCr-1 = 36, nCr = 84 and nC2r+1 = 36, than r is equal to
The number of positive integer which can be formed by using any number of digits from 0,1,2,3,4,5 but using each digit not more than once in each number is:
Using 7 consonant and 5 vowels, how many words consisting of 4 consonant and 3 vowels can be formed?
Ten different letters of an alphabet are give. Words with five letters are formed from given letter. The numbers of words which have at least one letter repeated is:
Five balls of different colours are to be placed in three boxes of different size. Each box can hold all five balls. In how many ways can we place the balls so that no box remains empty
If n-1C3 + n-1C4>nC3, then the least value of n is.
Six X’s have to be placed in the square of the figure given below such that each row contains at least one X. The number of ways in which his can be done is :
Four gents and two ladies can sit in a merry go round, and if the ladies are to sit side-by-side
A candidate is required to answer 6 out of 10 questions which are divided into two groups each containing five questions and he is not permitted to attempt more than 4 from each group. The number of ways, he can make up his choice is:
The greatest possible number of points of intersection of 8 straight lines and 4 circle is:
Delhi sub urban railway has 21 stations. Designating a ticket from one station to another station as distinct type of ticket, Calculate the number of types of tickets required for the railway services.
How many number can be formed with digits 1,2,3,4,3,2,1 so that odd digits always occupy the odd places?
The number of 3 digits numbers lying between 100 and 999 inclusive and having only odd digit occupy odd places?
In how many ways can examiner assign 30 marks to 8 questions giving not less than 2 marks to any questions?
There are five letter and 5 directed envelope. In how many ways can all the letter be put into the wrong envelope?
The number of odd integers between 1000 and 9909 with no digit repealed is :
|
27 docs|150 tests
|
Important Questions for Test:- Permutations And Combinations - 7
Test:- Permutations And Combinations - 7 MCQs with Answers
Online Tests for Test:- Permutations And Combinations - 7 Topic-wise Tests & Solved Examples for Mathematics
|
© EduRev
|
Education Revolution
|
|
