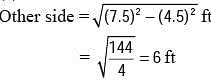Olympiad Test: Elementary Mensuration-I -1 - Class 7 MCQ
20 Questions MCQ Test Mathematics Olympiad Class 7 - Olympiad Test: Elementary Mensuration-I -1
The ratio between the length and the breadth of a rectangular park is 3 : 2. If a man cycling along the boundary of the park at the speed of 12 km/hr completes one round in 8 minutes, then the area of the park (in sq. m) is:
An error 2% in excess is made while measuring the side of a square. The percentage of error in the calculated area of the square is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The ratio between the perimeter and the breadth of a rectangle is 5 : 1. If the area of the rectangle is 216 sq. cm, what is the length of the rectangle?
The percentage increase in the area of a rectangle, if each of its sides is increased by 20%, is:
A rectangular park 60 m long and 40 m wide has two concrete crossroads running in the middle of the park and rest of the park has been used as a lawn. If the area of the lawn is 2109 sq. m, then what is the width of the road?
The diagonal of the floor of a rectangular closet is 7.5 feet. The shorter side of the closet is 4.5 feet. What is the area of the closet in square feet?
A towel, when bleached, was found to have lost 20% of its length and 10% of its breadth. The percentage of decrease in area is:
A man walked diagonally across a square plot. Approximately, what is the percent saved by not walking along the edges?
The diagonal of a rectangle is √41 cm and its area is 20 sq. cm. The perimeter of the rectangle must be:
What is the least number of squares tiles required to pave the floor of a room 15 m 17 cm long and 9 m 2 cm broad?
The difference between the length and breadth of a rectangle is 23 m. If its perimeter is 206 m, then its area is:
The length of a rectangle is halved, while its breadth is tripled. What is the percentage change in area?
The length of a rectangular plot is 20 metres more than its breadth. If the cost of fencing the plot @ 26.50 per metre is Rs 5300, what is the length of the plot in metres?
A rectangular field is to be fenced on three sides leaving a side of 20 feet uncovered. If the area of the field is 680 sq. feet, how many feet of fencing will be required?
A tank is 25 m long, 12 m wide and 6 m deep. The cost of plastering its walls and bottom at 75 paise per sq. m, is:
The area of playground is 1600 m2. What is the perimeter?
I. It is a perfect square playground.
II. It costs Rs 3200 to put a fence around the playground at the rate of Rs 20 per metre.
The area of a rectangle is equal to the area of right-angles triangle. What is the length of the rectangle?
I. The base of the triangle is 40 cm.
II. The height of the triangle is 50 cm.
What is the height of the triangle?
I. The area of the triangle is 20 times its base.
II. The perimeter of the triangle is equal to the perimeter of a square of side 10 cm.
What will be the cost of painting the inner walls of a room if the rate of painting is Rs 20 per square foot?
I. Circumference of the floor is 44 feet.
II. The height of the wall of the room is 12 feet.
What is the area of the hall?
I. Material cost of flooring per square metre is Rs 2.50.
II. Labour cost of flooring the hall is Rs 3500.
III. Total cost of flooring the hall is Rs 14,500.
|
24 videos|57 docs|102 tests
|
|
24 videos|57 docs|102 tests
|