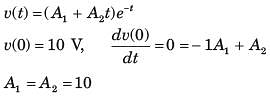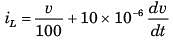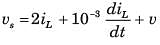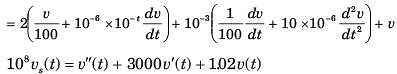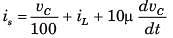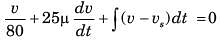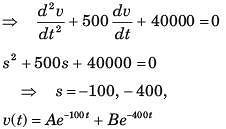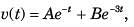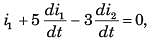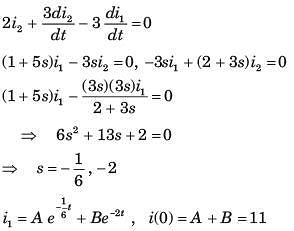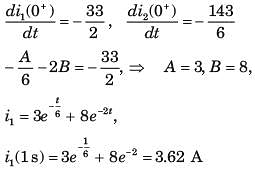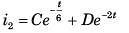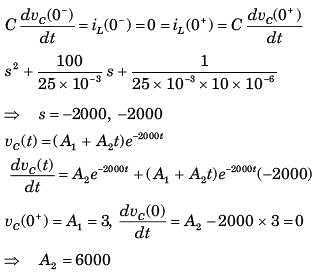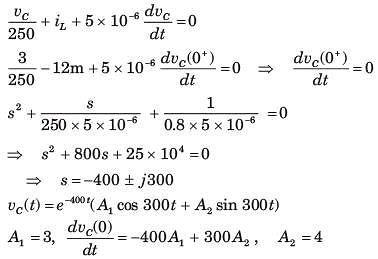Courses
Get the App Signup / Login

Test: Transient Response of DC & AC Networks - 1


10 Questions MCQ Test Network Theory (Electric Circuits) | Test: Transient Response of DC & AC Networks - 1


Description
This mock test of Test: Transient Response of DC & AC Networks - 1 for Electrical Engineering (EE) helps you for every Electrical Engineering (EE) entrance exam. This contains 10 Multiple Choice Questions for Electrical Engineering (EE) Test: Transient Response of DC & AC Networks - 1 (mcq) to study with solutions a complete question bank. The solved questions answers in this Test: Transient Response of DC & AC Networks - 1 quiz give you a good mix of easy questions and tough questions. Electrical Engineering (EE) students definitely take this Test: Transient Response of DC & AC Networks - 1 exercise for a better result in the exam. You can find other Test: Transient Response of DC & AC Networks - 1 extra questions, long questions & short questions for Electrical Engineering (EE) on EduRev as well by searching above.
QUESTION: 1

The natural response of an RLC circuit is described by the differential equation

The v(t) is

Solution:


QUESTION: 2

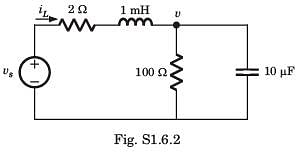
The differential equation for the circuit shown in fig. P1.6.2. is

Solution:



QUESTION: 3

The differential equation for the circuit shown in fig. P1.6.3 is

Solution:


QUESTION: 4

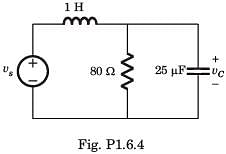
In the circuit of fig. P.1.6.4 vs = 0 for t > 0. The initial condition are v(0) = 6 V and dv(0) dt = -3000 Vs. The v(t) for t > 0 is
Solution:



A + B = 6, -100 A - 400B = -3000 ⇒  B = 8, A = -2

QUESTION: 5

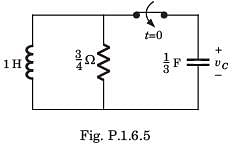
The circuit shown in fig. P1.6.5 has been open for a long time before closing at t = 0. The initial condition is v(0) = 2 V. The v(t) for t > is
Solution:

The characteristic equation is 
After putting the values, s2 +4s + 3 = 0

QUESTION: 6

Circuit is shown in fig. P.1.6. Initial conditions are i1(0) = i2(0) = 11A

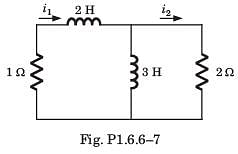
Q. i1 (1 s) = ?
Solution:



In differential equation putting t = 0 and solving

QUESTION: 7

Circuit is shown in fig. P.1.6. Initial conditions are i1(0) = i2(0) = 11A

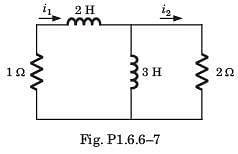
Q. i2 (1 s) = ?
Solution:


QUESTION: 8

vC(t) = ? for t > 0
Solution:


QUESTION: 9

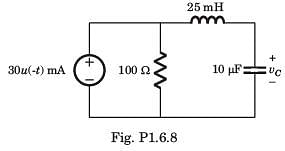
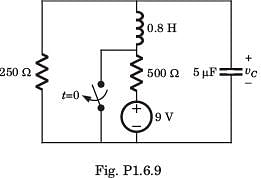
The circuit shown in fig. P1.6.9 is in steady state with switch open. At t = 0 the switch is closed. The output voltage vC(t) for t > 0 is
Solution:


QUESTION: 10

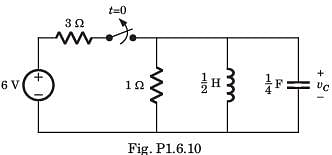
The switch of the circuit shown in fig. P1.6.10 is opened at t = 0 after long time. The v(t) , for t > 0 is
Solution:


Recommended Content

Recommended Tests

Similar Content

Related tests
Follow Us
© EduRev