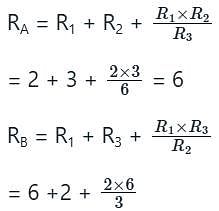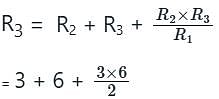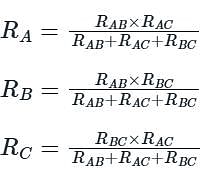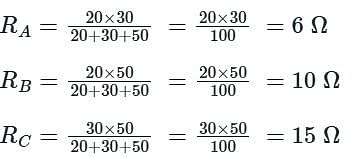Test: Delta Star & Star Delta - Electrical Engineering (EE) MCQ
20 Questions MCQ Test Network Theory (Electric Circuits) - Test: Delta Star & Star Delta
The value of the 3 resistances when connected in star connection is_________

Which, among the following is the right expression for converting from delta to star?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If a 6 ohm, 2ohm and 4ohm resistor is connected in delta, find the equivalent star connection.
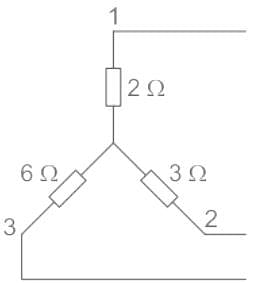
If a 4ohm, 3ohm and 2ohm resistor is connected in delta, find the equivalent star connection.
Which, among the following is the correct expression for star-delta conversion?
Rab is the resistance between the terminals A and B, Rbc between B and C and Rca between C and A. These 3 resistors are connected in star connection. After transforming to delta, the resistance at A will be?
If a 8/9ohm, 4/3ohm and 2/3ohm resistor is connected in star, find its delta equivalent.
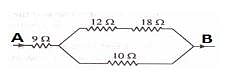
Find equivalent resistance between A & B in the circuit:
A balanced, delta-connected load has an impedance of 3∠30° Ω/phase. What will be the impedance of an equivalent star-connected load?
Which of the following is correct statement?
I. Star connection also be termed as 'T' connection
II. Delta connection can be termed as 'π'(pie) connection
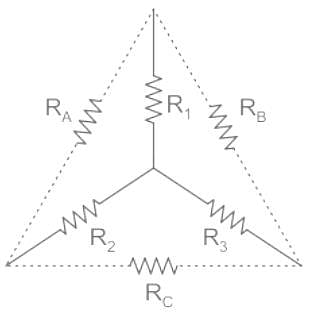
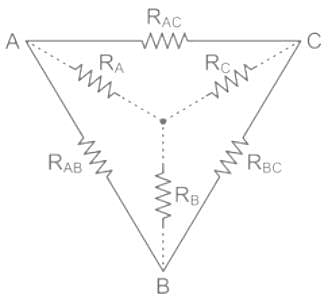
If the resistance in 'Δ' connected resistive network is R1, R2, R3 as shown in the figure,

then what will be the value of resistance 'Rx' in equivalent star network like?

Find DELTA equivalent resistance R12, R23, and R31 from the given STAR configuration.

The resistor value in a Y network that is equivalent to a Δ containing three resistors of R Ω each is:
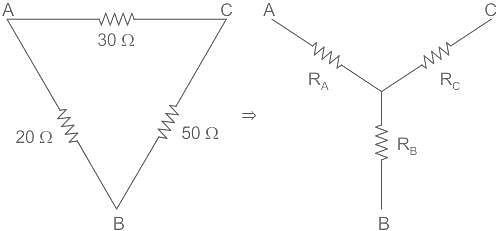
Three resistors, whose values are 20 Ω, 30 Ω, and 50 Ω, are connected in the delta connection. If the delta to star conversion is done, what will be the equivalent resistance used in the star combination?
|
68 videos|85 docs|62 tests
|
|
68 videos|85 docs|62 tests
|