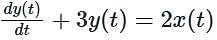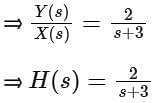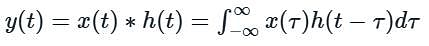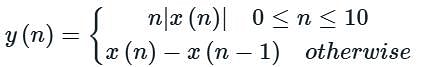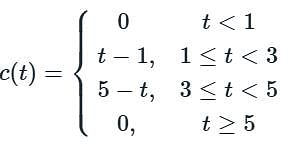Test: Properties of LTI Systems - Electrical Engineering (EE) MCQ
20 Questions MCQ Test Signals and Systems - Test: Properties of LTI Systems
Does the system h(t) = exp([-1-2j]t) correspond to a stable system?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
For an LTI discrete system to be stable, the square sum of the impulse response should be
Does the system h(t) = exp(-7t) correspond to a stable system?
What is the following expression equal to: h*(d+bd), d(t) is the delta function
The system transfer function and the input if exchanged will still give the same response.
In a discrete Linear Shift Invariant system the input sequence length is L, the impulse response sequence length is M, the output sequence length N is
A continuous-time system that is initially at rest is described by
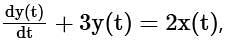
where x(t) is the input voltage and y(t) is the output voltage. The impulse response of the system is
The outputs of four systems (S1, S2, S3, and S4) corresponding to the input signal sin(t), for all time t, are shown in the figure.
Based on the given information, which of the four systems is/are definitely NOT LTI (linear and time-invariant)?

Which one of the following statements is NOT TRUE for a continuous time causal and stable LTI system?
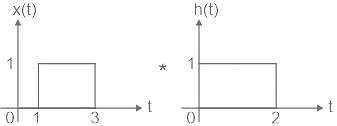
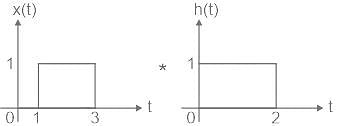
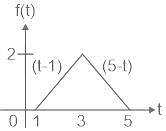
What is the convolution integral c(t) for a system with input x(t) and impulse response h(t), where x(t) = u(t - 1) - u(t - 3) and h(t) = u(t) - u(t - 2) ?
Consider a single input single output discrete-time system with x[n] as input and y[n] as output. Where the two are related as

Which one of the following statements is true about the system?
The signal y(t) = T{x(t)} = sin(2πt)⋆x(t) + u(t - 2) is _______.
Which one of the following statements is NOT TRUE for a continuous time causal and stable LTI system
Which of the following statements about the time-invariant and time-varying control systems is INCORRECT?
What is the convolution integral c(t) for a system with input x(t) and impulse response h(t), where x(t) = u(t - 1) - u(t - 3) and h(t) = u(t) - u(t - 2)?
|
41 videos|52 docs|33 tests
|
|
41 videos|52 docs|33 tests
|