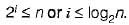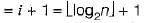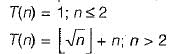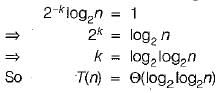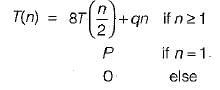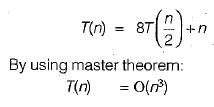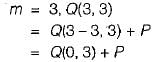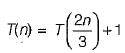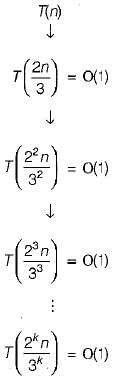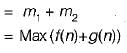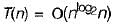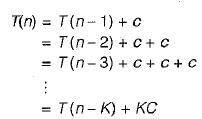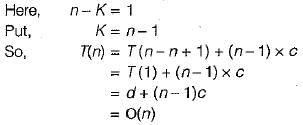Test: Algorithm Analysis & Asymptotic Notation- 2 - Computer Science Engineering (CSE) MCQ
15 Questions MCQ Test Question Bank for GATE Computer Science Engineering - Test: Algorithm Analysis & Asymptotic Notation- 2
Look at the following algorithms
int n;
int A[100];
void (x){
int i;
for (i=n/2;i > = 1; i -- )
y(i);
}
}
void y(int i)
{
.........;
.........;
.........;
}
Let complexity of y is O(log2n). Then the complexity of x will be
int n;
int A[100];
void (x){
for (i=n/2;i > = 1; i -- )
y(i);
}
}
void y(int i)
{
.........;
.........;
.........;
}
Let complexity of y is O(log2n). Then the complexity of x will be
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The time complexity of the following C function
is (assume n > 0)
int recursive (int n)
{
if (n == 1)
return(1);
else
return(recursive(n- 1) + recursive(n - 1));
}
is (assume n > 0)
int recursive (int n)
{
if (n == 1)
return(1);
else
return(recursive(n- 1) + recursive(n - 1));
}
The recurrence equation:
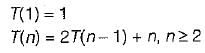
Evaluates to
Let T(n) be a function defined by the recurrence
T(n) - 2T(n/2) + √n for n≥2 and T(1) = 1
Which of the following statements is TRUE?
Suppose T(n) = 2T(n/2) + n, T(0) = T(1) = 1 Which one of the following is FALSE?
Consider the following segment of C code
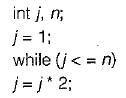
The number of comparisons made in the execution of the loop for any n > 0 is
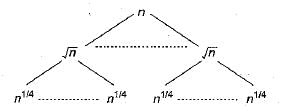
What is the time complexity of the following recursive function:
int DoSomething ( int n)
{
if {n< = 2)
return 1;
else
return DoSomething (floor (sqrt (n)))+n;
}
Using the standard algorithm, what is the time required to determine that a number n is prime?
The running time of an algorithm T(n), where ‘n’ is the input size is given by
T(n) = 8T(n/2) + qn. if n> 1
p, if n = 1
where p, q are constants. The order of this algorithm is
Let m, n be positive integers. Define Q(m, n) as
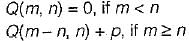
Then Q(m, 3) is (a div b, gives the quotient when a is divided by b)
T(n) = T(2n/3) + 1 then T(n) is equal to
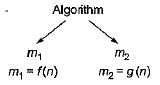
An algorithm is made up of 2 m odules m1 and m2. If order of M1 is f(n) and M2 is g(n) then the order of the algorithm is
The recurrence relation T(n) = mT(n/2) + an2 is satisfied by
The running time T(n) where ‘n' is the input size of a recursive algorithm is given as follow
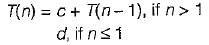
The order of this algorithm is
|
63 videos|8 docs|165 tests
|
|
63 videos|8 docs|165 tests
|




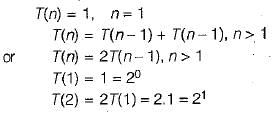

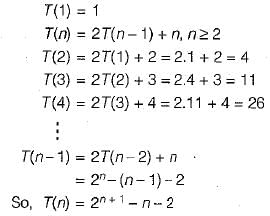
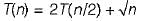
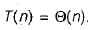
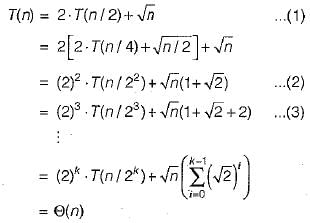
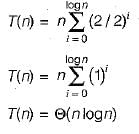
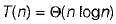 then it is also 0(n logn) and O(n2) but it is not Ω(n2).
then it is also 0(n logn) and O(n2) but it is not Ω(n2).