Test: Asymptotic Analysis of Algorithms- 2 - Computer Science Engineering (CSE) MCQ
20 Questions MCQ Test Question Bank for GATE Computer Science Engineering - Test: Asymptotic Analysis of Algorithms- 2
Randomized quicksort is an extension of quicksort where the pivot is chosen randomly. What is the worst case complexity of sorting n numbers using randomized quicksort?
Which one of the following is the recurrence equation for the worst case time complexity of the Quicksort algorithm for sorting n(≥ 2) numbers? In the recurrence equations given in the options below, c is a constant.
An unordered list contains n distinct elements. The number of comparisons to find an element in this list that is neither maximum nor minimum is
What is the size of the smallest MIS(Maximal Independent Set) of a chain of nine nodes?
If we use Radix Sort to sort n integers in the range (nk/2,nk], for some k>0 which is independent of n, the time taken would be?
The auxiliary space of insertion sort is O(1), what does O(1) mean ?
Suppose we want to arrange the ii numbers stored in an array such that all negative values occur before all positive ones. Minimum number of exchanges required in the worst case is:
The minimum number of record movements required to merge five files A (with 10 records), B (with 20 records), C (with 15 records), D (with 5 records) and E (with 25 records) is:
If one uses straight two-way merge sort algorithm to sort the following elements in ascending order 20, 47, 15, 8, 9, 4, 40, 30, 12, 17 then the order of these elements after the second pass of the algorithm is:
Consider the following C function definition.
int Trial (int a, int b, int c)
{
if ((a >= b) && (c < b) return b;
else if (a>=b) return Trial(a, c, b);
else return Trial(b, a, c);
}
The function Trial:
Consider the following program that attempts to locate an element x in a sorted array a[ ] using binary search. Assume N>1. The program is erroneous. Under what conditions does the program fail?
var i,j,k: integer; x: integer;
a: array; [1....N] of integer;
begin i:= 1; j:= N;
repeat
k:(i+j) div 2;
if a[k] < x then i:= k
else j:= k
until (a[k] = x) or (i >= j);
if (a[k] = x) then
writeln ('x is in the array')
else
writeln ('x is not in the array')
end;
Match the following:
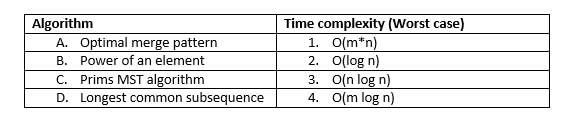
Which of the following option is correct?
Consider the program
void function(int n) {
int i, j, count=0;
for (i=n/2; i <= n; i++)
for (j = 1; j <= n; j = j*2)
count++;}
The complexity of the program is
If b is the branching factor and m is the maximum depth of the search tree, what is the space complexity of greedy search?
The time complexity of computing the transitive closure of a binary relation on a set of n elements is known to be
A recursive function h, is defined as follows :
h(m) = k, if m = 0
= 1, if m = 1
= 2 h(m – 1) + 4h(m – 2), if m ≥ 2
If the value of h(4) is 88 then the value of k is :
Match the following with respect to algorithm paradigms :

|
63 videos|8 docs|165 tests
|
|
63 videos|8 docs|165 tests
|





















