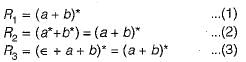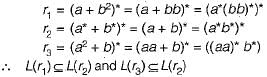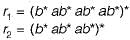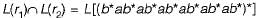Test: Finite Automata: Regular Languages- 2 - Computer Science Engineering (CSE) MCQ
15 Questions MCQ Test Question Bank for GATE Computer Science Engineering - Test: Finite Automata: Regular Languages- 2
Which of the following statements are true?
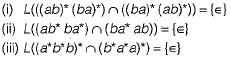
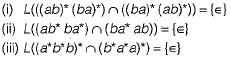
Which of the following statements are true?
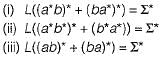
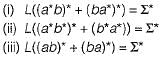
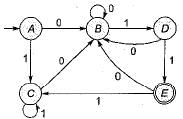
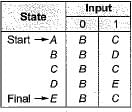
If a DFA is represented by the following transition table, then how many states does the corresponding minimal DFA contains?

Consider G = {(a, b), {S}, S, |S→b|Sa|aS|SS}) Which of the following are true?
(i) aabbaa ∈ G
(ii) G is ambiguous
(iii) Regular expression corresponding to G is ba*
How many languages are over the alphabet R?
Which of the following statements are false?
Which of the following statement must always be true for A and B? Suppose A and B are two sets of strings from ∑*, such that 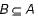
(i) if A is finite then, B is finite.
(ii) If A is regular then, S is regular.
(iii) If A is context free then, B is context free,
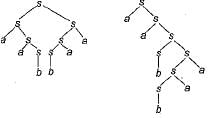
Consider the following grammar G:
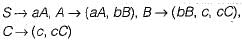
Which of the following is L(G)?
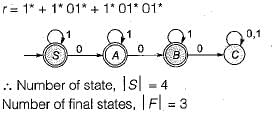
Deterministic finite automata of a language over alphabets {0, 1), which does not contain 3 consecutive 0’s. Minimum how many states, S, in all, the DFA will have and how many of them will be final states, F?
Consider the following regular grammar:
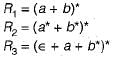
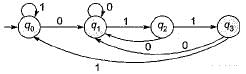
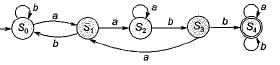
Minimized deterministic finite automata of which R1, R2 and R3 are exactly same except state names?
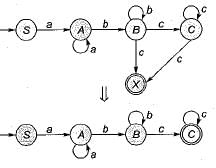
Consider the following machine M:
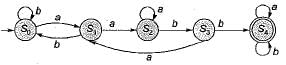
What is the language L(M) accepted by this machine?
Let r1 = (a + b2)*, r2 = (a* + b*)*, r3 = (a2 + b)*. Which of the following is true?
r1 = {b* ab* ab* ab*)*, r2 = (b* ab* ab*)*. What is L(r1) ∩ L(r2)?
Which of the following statement is not correct?
|
73 videos|8 docs|165 tests
|
|
73 videos|8 docs|165 tests
|