Test: Mathematical Logic- 1 - Electrical Engineering (EE) MCQ
10 Questions MCQ Test GATE Electrical Engineering (EE) Mock Test Series 2025 - Test: Mathematical Logic- 1
If the proposition¬ p ⇒ q is true, then the truth value of the proposition ¬ p v (p ⇒ q), where ¬ is negation, 'v' is inclusive or and '⇒’ is implication, is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let a, b, c, d be propositions. Assume that the equivalence a ⇔ ( bv ¬ b) and b ⇔ c hold. Then the truth-value of the formula (a ∧ b) → (a ∧ c) v d is always
The following propositional statement is
(P → (Q v R)) → (( P ∧ Q) → R)
A logical binary relation  is defined as follows:
is defined as follows:
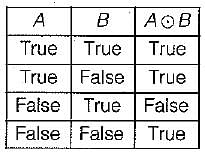
Let ~ be the unary negation (NOT) operator, with higher precedence, than  Which one of the following is equivalent to A ∧ B?
Which one of the following is equivalent to A ∧ B?
Which of the following is TRUE about formulae in Conjunctive Normal Form?
The binary operation is defined as follows:
is defined as follows:

Which one of the following is equivalent to P v Q?
Consider the following well-formed formulae:
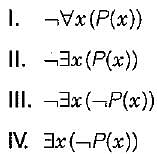
Which of the above are equivalent?
Which one of the following is NOT logically e quivalent to 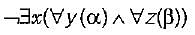
The CORRECT formula for the sentence, "not all rainy days are cold” is
|
25 docs|247 tests
|
|
25 docs|247 tests
|


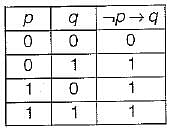


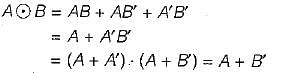
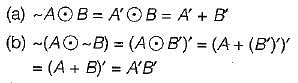



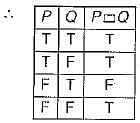
 Q more efficiently, in conjunctive normal form.
Q more efficiently, in conjunctive normal form. Q = P + Q' (the max -term corresponding to the third row, where the function is false).
Q = P + Q' (the max -term corresponding to the third row, where the function is false).
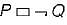 is equivalent to P+ Q.
is equivalent to P+ Q.
















