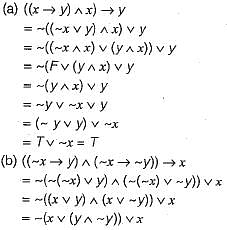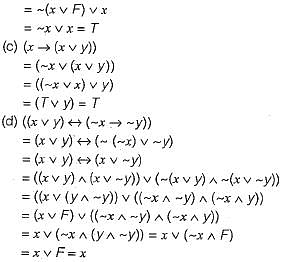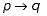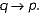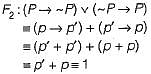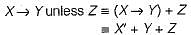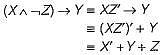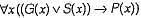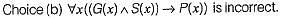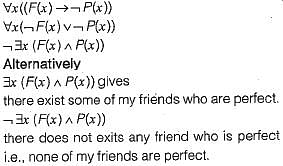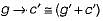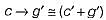Test: Mathematical Logic- 2
13 Questions MCQ Test GATE Electrical Engineering (EE) 2023 Mock Test Series | Test: Mathematical Logic- 2
| 1 Crore+ students have signed up on EduRev. Have you? |
Which one of the following is false? Read ∧ as AND, v as OR, ~ as NOT, → as one way implication and 
as two way implication.
as two way implication.
What is the converse of the following assertion?
I stay only if you go
I stay only if you go
Let p : l stay
q ; you go
I stay only if you go
Converse of 
Now convert the answers one-by-one into boolean form. Only option (a) i.e. “1 stay if you go” converts to 
Consider two well-formed formulas in propositional logic:
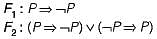
Which of the following statements is correct?
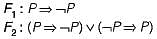
Which of the following statements is correct?
So F1 is contingency. Hence, F1 is satisfiable but not valid.
So F2 is tautology and therefore valid.
“If X then Y unless Z” is represented by which of the following formulas in propostional logic? ("_") is negation, “∧” is conjunction, and "→" is implication)
If X then Y unless Z is represented by
Now convert the answers one-by-one into boolean form only choice (a) converts to X'+ Y + Z as can be seen below:
Let P, Q and, R be three atomic propositional assertions. Let X denote ( P v Q ) → R and Y denote (P → R) v (Q → R). Which one of the following is a tautology?
Which one of the following is the most appropriate logical formula to represent the statement:
“Gold and silver ornaments are precious”
The following notations are used:
G(x): x is a gold ornament
S(x): x is a silver ornament
P(x): x is precious
The correct translation of "Gold and silver ornaments are precious ” is choice (d)
which is read as “if an ornament is gold or silver, then it is precious”.
Now since a given ornament cannot be both gold and silver at the same time.
Suppose the predicate P(x, y, t) is used to represent the statement that person x can fool person y at time t. Which one of the statements below expresses best the meaning of the formula
≡ it is not true that (someone can fool all people at all time)
≡ no one can fool everyone all the time
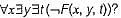
What is the logical translation of the following statements?
“None of my friends are perfect"
None of my friends are perfect i.e., all of my friends are not perfect
Consider the statement:
"Not all that glitters is gold"
Predicate glitters (x) is true if x glitters and predicate gold (x) is true if x is gold. Which one of the following logical formulae represents the above statement?
There exist gold which is not glitter i.e. not all golds are glitters.
Not all that glitters is gold i.e., there exist some which glitters and which is not gold.
Which one of the following propositional logic formulas is TRUE when exactly two of p, q, and r are TRUE?
This is exactly the min-term form of a logical formula which is true when exactly two variables are true (only p, q true or only p, r true or only q, r true).
Which one of the following Boolean expressions is NOT a tautology?
Consider the following statements:
P : Good mobile phones are not cheap
Q : Cheap mobile phones are not good
L : P implies Q
M : Q implies P
N : P is equivalent to Q
Which one of the following about L, M and N is CORRECT?
g : mobile is good
c : mobile is cheap
P : Good mobile .phones are not cheap
Q : Cheap mobile phones are not good
∴ Both P and Q are equivalent.
Since both P and Q are equivalent, all three of L, M, N are true.
Consider the following two statements:
S1: If a candidate is known to be corrupt, then he will not be elected.
S2: If a candidate is kind, he will be elected.
Which one of the following statements follows from S1 and S2 as per sound inference rules of logic?
C : Person is corrupt
K : Person is kind.
E : Person is elected
|
22 docs|274 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
22 docs|274 tests
|
Download free EduRev App
Related content with Test: Mathematical Logic- 2
|
|
|
|
Related tests with Test: Mathematical Logic- 2
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
