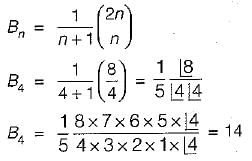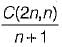Test: Trees- 2 - Computer Science Engineering (CSE) MCQ
15 Questions MCQ Test Question Bank for GATE Computer Science Engineering - Test: Trees- 2
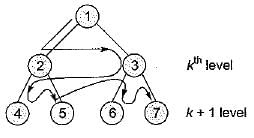
Level order traversal of a rooted tree can be done by starting from the root and performing
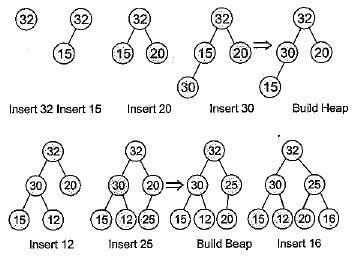
The elements 32, 15, 20, 30, 12, 25, 16 are inserted one by one in the given order into a maxHeap. The resultant maxHeap is
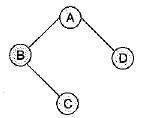
Which one of the following binary trees has its inorder and preorder traversals as BCAD and ABCD, respectively?
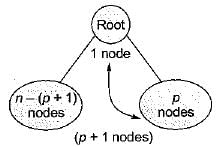
The numbers 1 , 2 .... n are inserted in a binary search tree in some order, In the resulting tree, the right subtree of the root contains p nodes. The first number to be inserted in the tree must be
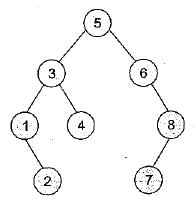
A binary search tree contains the numbers 1,2, 3, 4, 5, 6, 7, 8, When the tree is traversed in preorder and the values in each node printed out, the sequence of values obtained is 5, 3,1, 2, 4, 6, 8, 7. If the tree is traversed in postorder, the sequence obtained would be
How many distinct binary search trees can be created out of 4 distinct keys?
In a complete k-ary, every internal node has exactly k children. The number of leaves in such a tree with n internal nodes is
In a binary max heap containing.n numbers, the smallest element can be found in time
In a binary tree, the number of internal nodes of degree 1 is 5, and the number of internal nodes of degree 2 is 10. The number of leaf nodes in the binary tree is
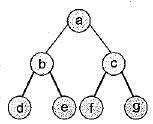
The inorder and preorder traversal of a binary tree are “dbeafcg" and “abdecfg’’ respectively. The postorder traversal of the binary tree is
Consider the process of inserting an element into a Max Heap, where the Max Heap is represented by an array. Suppose we perform a binary search on the path from the new leaf to the root to find the position for the newly inserted element, the number of comparisons performed is
What is the maximum height of any AVL-tree with 7 nodes? Assume that the height of a tree with a single node is 0.
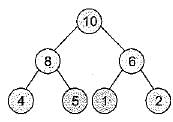
A max-heap is a heap where the value of each parent is greater than or equal to the value of its children. Which of the following is a max-heap?
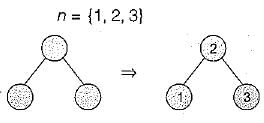
We are given a set of n distinct elements and an unlabeled binary tree with n nodes. In how many ways can we populate the tree with the given set so that it becomes a binary search tree?
|
73 videos|8 docs|165 tests
|
|
73 videos|8 docs|165 tests
|